2. 农业部南方耕地污染防控重点实验室,湖南 长沙 410128
2. Key Laboratory of Southern Farmland Pollution Prevention and Control, Ministry of Agriculture, Changsha, Hunan 410128, China
近年来,我国大部分城市正遭遇严重的大气污染问题,大气环境质量受到严重影响,特别是以细颗粒物(PM2.5)和臭氧(O3)为首要污染物的重污染天气过程频发,对人体健康和社会经济造成严重影响[1]。随着人们对良好居住环境的迫切需要以及社会关注度的不断提高,对空气质量预测准确度的需求也日益增加[2]。
环境空气质量一方面受人类活动(工业生产、机动车出行、城市建设等)的影响,另一方面也受自然因素(气象、地形地貌等)的影响[3-4],这些因素增加了空气质量实时精准预测预报的不确定性。目前,我国现行的城市环境空气质量预报模型主要为数值预报和统计预报模型[5-6]。数值预报模型包括嵌套网格空气质量预报系统(NAQPMS)、区域多尺度空气质量模型(CMAQ)、扩展的综合空气质量模型(CAMx)、区域气象-大气化学在线耦合模型(WRF-Chem)等,对模型参数、污染源清单、大气物理化学反应机理等依赖性较强,且污染源的污染物排放动态变化较大,较难获得精确的污染源数据,使得数值预报模型在计算过程中容易出现偏差。而统计预报模型则是利用环境气象数据和环境空气污染物监测数据建立的统计模型,如人工神经网络模型、多元线性回归模型、自由回归滑动平均模型(ARMA)等,统计预报模型能有效避免数值预报模型的弊端,具有运算量少、易于操作等优点[5, 7]。
人工神经网络是基于生物学中神经网络的基本原理,具有高度的非线性特点,能够进行复杂的逻辑操作和非线性关系系统的实现,反向传播神经网络(BP神经网络)模型是其中应用最广泛的一类。高愈霄等[8]应用BP神经网络模型对京津冀及周边城市、汾渭平原、苏皖鲁豫交界地区和长三角地区的PM2.5质量浓度进行预测,平均误差均值为19~31 μg/m3,标准化平均偏差总体呈系统性正向偏差,均值为9%~18%。朱苹等[9]利用BP神经网络模型对合肥市PM2.5质量浓度进行预测,一致性指数为84%,相关系数为0.73。BP神经网络模型中输入因子的选取对预测结果具有较大影响,目前大多数研究主要考虑气象因素,朱苹等[9]在模型中仅考虑了气象因素,高愈霄等[8]在模型中考虑了气象因素和PM2.5质量浓度的影响。
目前,我国大部分城市的空气质量呈现出明显的以PM2.5和O3为主的复合污染特点[7]。氮氧化物(NOX)是PM2.5和O3的重要前体物,且随着机动车保有量的增加和固定污染源排放量的减少,NOX对PM2.5和O3生成的贡献也越来越大。同时,PM2.5中二次组分占比越来越高,而二次组分的形成受大气氧化性影响极大。然而,现有的BP神经网络模型应用中却极少考虑大气氧化性因素的影响,因此亟须开展相关研究[10-11]。
郑州市是我国中原城市群的核心城市之一,空气质量问题受到极大关注。现应用BP神经网络模型建立了郑州市不同季节的PM2.5预报模型,对后1日PM2.5质量浓度进行预报,并对模型预报结果进行评价。除考虑传统的气象因素外,同时考虑了大气氧化性因素对PM2.5的影响,以提高预报结果的准确性。并通过对比加入大气氧化性因素前后的模型结果,探究统计预报方法对不同季节PM2.5预报的可行性,以期为完善预报模型和推进统计预报方法的应用提供支持。
1 材料与方法 1.1 数据来源采用2017年1月1日—2022年2月28日郑州市环境空气质量逐日质量浓度监测数据(中国环境监测总站发布)和同期气象数据(中国气象数据网发布),剔除异常及空缺数据后,剩余有效数据共1 725组。将各季节前80%的数据构成训练集,后20%的数据构成测试集[12],最终春季数据383组(训练集306组,测试集77组),夏季数据431组(训练集345组,测试集86组),秋季数据437组(训练集350组,测试集87组),冬季数据474组(训练集379组,测试集95组)。
1.2 数据预处理神经网络训练对输入数据具有一定的依赖性,为了避免因数据单位及数量级等差异造成的影响,需要对原始数据进行归一化处理,获得无量纲序列[13-14],最终将矩阵的每一行归一到[0, 1]之间,采用的归一化方法见式(1)。
| $ X_i=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }} $ | (1) |
式中:Xi——归一化后得到的数值;xi——原始数值;xmin——原始数值最小值;xmax——原始数值最大值。
1.3 BP神经网络模型原理及参数设置BP神经网络主要是利用输入样本集和输出样本集数据进行训练,使网络达到给定的输入输出映射函数关系,可以实现从输入到输出的任意非线性映射,网络主要特点是信号前向传递和误差反向传播[12]。BP神经网络由输入层、隐含层和输出层3层基本结构构成,本文构建的BP神经网络初步选定1个输入层,1个隐含层和1个输出层。
现利用MATLAB软件的默认神经网络的配置程序构建神经网络模型,选取贝叶斯正则化算法(trainbr)为训练算法。根据前期研究并参考相关文献,选取对环境空气PM2.5质量浓度影响较大的气象参数,主要包括温度、相对湿度、风速和风向等[15],因此,为实现对郑州市后1日PM2.5质量浓度的预测,选取当日最低温度、最高温度、相对湿度和风级4个气象参数和前1日的PM2.5质量浓度监测数据作为模型备选因子。同时,考虑大气氧化性因素对PM2.5的影响,但由于大气主要的氧化剂OH·难以直接测量,常以OX(NO2+O3)表征大气氧化性[16-18],将二氧化氮(NO2)和O3作为评价大气氧化能力的指标[19]。因此,除气象因子外,还将前1日的NO2和O3日最大8 h滑动平均值(O3-8 h)数据作为因子加入模型,最终输出数据为当日PM2.5日均质量浓度。本研究最终设定2种情景:考虑大气氧化性因素(情景一)和不考虑大气氧化性因素(情景二),并对不同情景下的预测结果分别进行评价,以探究加入大气氧化性因素是否对城市PM2.5质量浓度的预报具有优化效果。
研究表明,隐含层节点数较少时会使神经网络出现“欠拟合”现象,过多会出现“过拟合”现象。隐含层节点数可以参照公式(2)来确定[20-21]:
| $ n=\sqrt{a+b+c} $ | (2) |
式中:n——隐含层节点数;a——输入层节点数;b——输出层节点数;c——1~10之间的常数。
本研究输入层节点数为5和7,输出层节点数为1,因此初始选取隐含层节点数为4~13,针对不同隐含层对网络进行训练,依据网络性能参数均方误差(MSE)指标评估不同网络的预报效果,MSE值越小,表明网络预报结果越好。经过在不同隐含层节点数情景下调试,春季、夏季、秋季最终选取隐含层节点数为4层,冬季最终选取隐含层节点数为5层。
1.4 评价方法预报结果评价方法采取标准化平均偏差(NMB)、均方根误差(RMSE)、相关系数(r)、一致性指数(IA)、准确率(Q)和级别预报准确率(G)指标[8-9, 22-23]。NMB反映的是各个预报质量浓度与实况质量浓度的偏离程度,RMSE反映的是预报质量浓度与实况质量浓度的偏离程度,NMB和RMSE绝对值越小,说明预报值和实况值误差越小,预报效果越好;r值、IA和Q值越大,表示预报效果越好;此外,参考空气质量预报评估相关文件对G值进行评估,即PM2.5对应空气质量分指数级别预报准确天数与总天数的百分比。计算方法见式(3)—(8)。
| $ {\rm{NMB}} = \frac{{\frac{1}{N}\sum\limits_{i = 1}^N {\left( {{F_i} - {O_i}} \right)} }}{{\frac{1}{N}\sum\limits_{i = 1}^N {{O_i}} }} $ | (3) |
式中:NMB——标准化平均偏差,%;N——参与计算的样本对个数;Fi——第i个样本对中污染物预报质量浓度,μg/m3;Oi——第i个样本对中,污染物实况质量浓度,μg/m3。
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(F_i-O_i\right)^2} $ | (4) |
式中:RMSE——均方根误差,μg/m3;N、Fi和Oi同上。
| $ r = \frac{{\sum\limits_{i = 1}^N {\left( {{F_i} - \bar F} \right)} \sum\limits_{i = 1}^N {\left( {{O_i} - \bar O} \right)} }}{{\sqrt {\sum\limits_{i = 1}^N {{{\left( {{F_i} - \bar F} \right)}^2}} } \sqrt {\sum\limits_{i = 1}^N {{{\left( {{O_i} - \bar O} \right)}^2}} } }} $ | (5) |
式中:r——相关系数;F——参与计算的污染物预报质量浓度平均值,μg/m3;O——参与计算的污染物实况质量浓度平均值,μg/m3;N、Fi和Oi同上。
| $ {\rm{IA}} = 1 - \left[ {\frac{{\sum\limits_{i = 1}^N {{{\left( {{F_i} - {O_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {{{\left( {\left| {{F_i} - \bar O} \right| + \left| {{O_i} - \bar O} \right|} \right)}^2}} }}} \right] $ | (6) |
式中:IA——一致性指数,%;N、Fi、Oi和O同上。
| $ Q=1-\frac{\left|F_i-O_i\right|}{O_i} \times 100 \% $ | (7) |
式中:Q——准确率,%;Fi和Oi同上。
| $ G = \frac{{\sum\limits_{i = 1}^N {{d_i}} }}{{\sum\limits_{i = 1}^N {{D_i}} }} $ | (8) |
式中:G——级别预报准确率,%;i——空气质量分指数(IAQI)级别,级别总数为6级;di——级别预报准确天数, d;Di——污染物实况质量浓度对应的IAQI级别为i的总天数,d; N同上。
2 结果与讨论 2.1 模型预报结果分析采用trainbr训练算法构建BP神经网络预报模型,经过多次神经网络训练,最终选择相对较优的结果进行预报模型的构建,各季节训练结果见表 1。
| 表 1 各季节训练结果 |
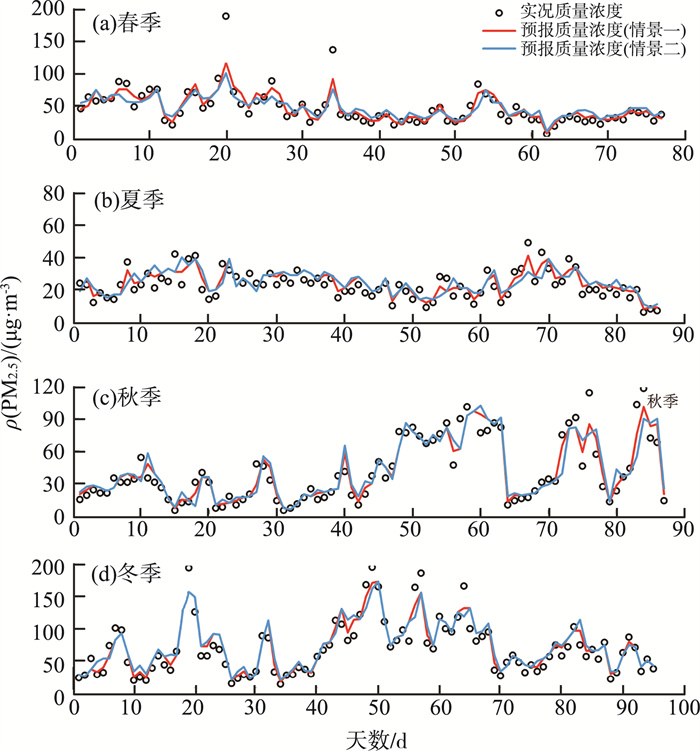
将测试集数据输入预报模型进行预测,得到PM2.5预报质量浓度结果,与实况质量浓度进行对比分析,各季节PM2.5实况质量浓度与预报质量浓度对比见图 1(a)—(d)。
|
图 1 各季节PM2.5实况质量浓度与预报质量浓度对比 |
由图 1可见,各季节PM2.5预报质量浓度与实况质量浓度整体趋势较为一致,相对于情景二,情景一的PM2.5预报质量浓度趋势与实况质量浓度更加吻合。但是无论哪种情景,对于沙尘天气等突发因素和区域传输导致的PM2.5质量浓度突发性升高情况,模型预报效果稍有不足。
2.2 模型预报效果分析 2.2.1 模型预报效果分布春季、夏季、秋季和冬季的PM2.5实况质量浓度均值分别为47.1,22.9,41.6和71.1 μg/m3,情景一的PM2.5预报质量浓度均值分别为47.3,24.1,41.7和74.6 μg/m3,情景二的PM2.5预报质量浓度均值分别为47.7,24.7,42.4和76.9 μg/m3。4个季节的PM2.5预报平均质量浓度与实况平均质量浓度偏差相对较小,表明模型对各季节PM2.5质量浓度的整体预报效果较好,其中情景一的各季节PM2.5预报质量浓度更接近实况质量浓度。
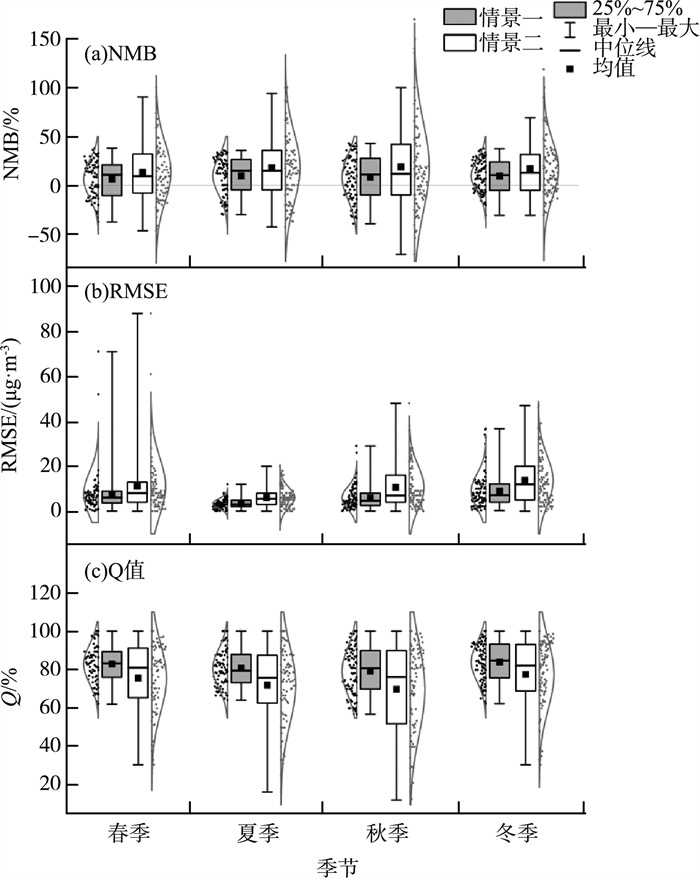
各季节测试集样本预报效果分布见图 2(a)—(c)。
|
图 2 各季节测试集样本预报效果分布 |
由图 2可见,2种情景下各季节大部分样本对的NMB为正数,中位数和平均值均 > 0,表明大部分样本存在一定的高估[8],但偏差均处于相对较低水平,且各季节情景一的NMB相对小于情景二。2种情景下的RMSE除春季、秋季和冬季个别样本对相对略高外,其余大部分样本对均处于较低水平,各季节情景一的RMSE相对小于情景二,其中情景一春季、夏季和秋季RMSE的第75百分位均 < 10 μg/m3。较低的NMB和RMSE表明,各季节预报结果具有较好的稳定性,其中情景一的预报效果更稳定,表明增加大气氧化性因素可以对模型进行优化。2种情景下各季节样本对的Q值均处于较高水平,表明2种情景对各季节预报结果较为准确。情景一除秋季个别样本对外,其余样本对的Q值均 >60%,且各季节Q值的第25百分位均 > 70%,其中冬季、春季和秋季的Q值中位数均 > 80%,表明情景一的预报结果具有更好的准确性。
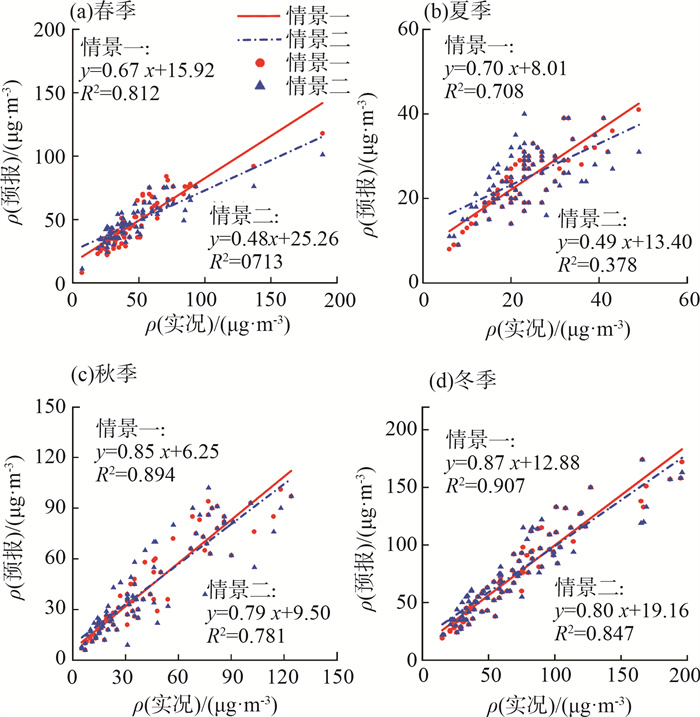
2.2.2 模型预报线性拟合各季节PM2.5实况质量浓度与预报质量浓度散点图和线性拟合情况见图 3(a)—(d)。
|
图 3 各季节PM2.5实况质量浓度与预报质量浓度散点图和线性拟合情况 |
由图 3可见,情景一4个季节拟合曲线的R2分别为0.812,0.708,0.894和0.907,情景二4个季节拟合曲线的R2分别为0.713,0.378,0.781和0.847。2种情景均表现出冬季拟合程度最高,秋季次之,最后为春季和夏季的特征,且情景一4个季节的PM2.5预报质量浓度与实况质量浓度的拟合效果均优于情景二的拟合效果。
2.2.3 模型预报效果评价为了评价2种情景下各季节模型预报效果,利用NMB、RMSE、r值、IA、Q值和G值指标对各季节模型预报结果进行整体评价,各季节模型预报评价结果见表 2。
| 表 2 各季节模型预报评价结果 |
由表 2可见,2种情景下各季节PM2.5预报质量浓度与实况质量浓度的NMB总体均呈正向偏差,表明总体存在一定的高估。其中情景一夏季NMB最大,为5.2%,其次为冬季(5.0%)、春季(0.5%)和秋季(0.4%),表明情景一夏季预报结果正向偏差最大,秋季预报结果正向偏差最小。情景二夏季NMB最大,为7.5%,其次为冬季(6.9%)、秋季(1.9%)和春季(1.3%),表明情景二夏季预报结果正向偏差最大,春季预报结果正向偏差最小。2种情景下PM2.5预报质量浓度与实况质量浓度的RMSE夏季最低,分别为4.7和7.0 μg/m3,其次为秋季(9.8和14.0 μg/m3)、春季(12.5和16.4 μg/m3)和冬季(13.2和17.0 μg/m3)。综上,2种情景下各季节PM2.5预报质量浓度与实况质量浓度的NMB和RMSE均处于相对较低水平,表明2种情景的预报效果均具有较好的稳定性。
2种情景下各季节预报质量浓度与实况质量浓度的r值和IA均处于相对较高水平。情景一的r值均 > 0.8,IA均 > 90%;情景二的r值均 > 0.6,IA均 > 75%。2种情景的r值和IA均为冬季最高,秋季次之,最后为春季和夏季。情景一各季节的Q值均>79%,且2种情景的Q值均表现为冬季最高,分别为84.0%和77.6%,其次为春季(83.0%和75.7%)、夏季(80.8%和72.1%)和秋季(79.3%和69.9%)。情景一各季节的G值均 > 80%,其中夏季高达91.9%;情景二各季节的G值均 > 70%。综上,2种情景下各季节的r值、IA、Q值和G值均处于相对较高水平,表明PM2.5实况质量浓度与预报质量浓度趋势较为一致,吻合程度较高。
情景一各季节PM2.5预报质量浓度与实况质量浓度的NMB和RMSE均低于情景二。其中夏季NMB降低了2.3%,其次为冬季(1.9%)、秋季(1.5%)、春季(0.8%);秋季RMSE降低了4.2 μg/m3,其次为春季(3.9 μg/m3)、冬季(3.8 μg/m3)、夏季(2.3 μg/m3)。情景一各季节PM2.5预报质量浓度与实况质量浓度的r值、IA、Q值和G值均高于情景二。其中夏季的r值提高了36.1%,其次为秋季(6.9%)、春季(6.5%)、冬季(3.5%);夏季IA提高了14.6%,其次为春季(8.5%)、秋季(3.4%)、冬季(2.2%);秋季Q值提高了9.4%,其次为夏季(8.7%)、春季(7.3%)、冬季(6.4%);春季G值提高了9.1%,其次是秋季(8.1%)、冬季(7.4%)、夏季(3.5%)。综上,在情景一下,模型对各季节PM2.5质量浓度整体的预测效果相对更优。
2.3 预报偏差讨论(1) BP神经网络模型偏差主要取决于构建模型时输入的数据、神经网络设计、模型算法等[24]。本文构建的BP神经网络模型在实现预报时需要输入气象数据和污染物质量浓度监测数据。其中污染物质量浓度监测数据为实测数据,偏差相对较低;而气象数据为预报数据,存在不同程度的偏差。
(2) 对比不考虑大气氧化性因素和考虑大气氧化性因素的预报效果。在复合大气污染和二次组分贡献增加的情况下,考虑大气氧化性因素可以对模型进行优化。但对于突发性事件(沙尘和外来传输)导致的PM2.5质量浓度突发性升高情况,模型预报效果还有待完善。
3 结论(1) 针对郑州市4个季节,构建了考虑大气氧化性因素(情景一)和不考虑大气氧化性因素(情景二)2种情景的BP神经网络模型用以对空气质量进行预报。结果表明,2种情景下各季节PM2.5预报质量浓度与实况质量浓度的NMB和RMSE均处于较低水平,表明2种情景对各季节PM2.5质量浓度的预报效果具有较好的稳定性;各季节PM2.5预报质量浓度与实况质量浓度的r值、IA、Q值和G值均处于相对较高水平,表明实况质量浓度与预报质量浓度趋势较为一致,吻合程度较高。
(2) 情景一各季节PM2.5预报质量浓度与实况质量浓度的NMB和RMSE均低于情景二,降幅分别为0.8%~2.3%和2.3~4.2 μg/m3;情景一各季节PM2.5预报质量浓度与实况质量浓度的r值、IA、Q值和G值均高于情景二,增幅分别为3.5%~36.1%,2.2%~14.6%,6.4%~9.4%和3.5%~9.1%。以上结果表明,考虑大气氧化性因素能够优化模型对PM2.5质量浓度的预报效果。
(3) 利用气象资料和大气氧化性因素等数据资料构建的BP神经网络模型能够较好地实现对城市后1日PM2.5质量浓度的预报,为探究统计预报模型在城市PM2.5预报中的可行性提供参考。由于环境空气中不同污染物的主要影响因素不尽相同,因此利用BP神经网络开展城市环境空气中其他污染物预报将成为下一步的研究重点。
| [1] |
王文兴, 柴发合, 任阵海, 等. 新中国成立70年来我国大气污染防治历程、成就与经验[J]. 环境科学研究, 2019, 32(10): 1621-1635. |
| [2] |
卢亚灵, 李勃, 范朝阳, 等. 空气质量预测模拟技术演变与发展研究[J]. 中国环境管理, 2021, 13(4): 84-92. |
| [3] |
佟彦超. 中国重点城市空气污染预报及其进展[J]. 中国环境监测, 2006, 22(2): 69-71. |
| [4] |
朱晏民, 徐爱兰, 孙强. 基于深度学习的空气质量预报方法新进展[J]. 中国环境监测, 2020, 36(3): 10-18. |
| [5] |
宋鹏程, 张馨文, 黄强, 等. 我国城市环境空气质量预报主要模型及应用[J]. 四川环境, 2019, 38(3): 70-76. |
| [6] |
王淑莹, 许荣, 尹翠芳, 等. 基于OPAQ的城市空气质量预报系统研究[J]. 中国环境监测, 2016, 32(3): 13-20. |
| [7] |
HE J J, GONG S L, YU Y, et al. Air pollution characteristics and their relation to meteorological conditions during 2014—2015 in major Chinese cities[J]. Environmental Pollution, 2017, 223: 484-496. |
| [8] |
高愈霄, 汪巍, 黄永海, 等. 基于神经网络和数值模型的重点区域PM2.5预报比较分析[J]. 环境科学, 2022, 43(2): 663-674. |
| [9] |
朱苹, 王成刚, 冯妍, 等. 合肥市冬季PM2.5统计预报方法初试与比较研究[J]. 环境科学与技术, 2019, 42(12): 81-89. |
| [10] |
李泽群, 韦骏. 利用人工智能神经网络预测广州市PM2.5日浓度[J]. 北京大学学报(自然科学版), 2021, 27(4): 645-652. |
| [11] |
张怡文, 郭傲东, 吴海龙, 等. 基于PCA-BP神经网络的PM2.5季节性预测方法研究[J]. 南京林业大学学报(自然科学版), 2020, 44(5): 231-238. |
| [12] |
申浩洋, 韦安磊, 王小文, 等. BP人工神经网络在环境空气SO2质量浓度预测中的应用[J]. 环境工程, 2014, 32(6): 117-121. |
| [13] |
白鹤鸣, 沈润平, 师华定, 等. 基于BP神经网络的空气污染指数预测模型研究[J]. 环境科学与技术, 2013, 36(3): 186-189. |
| [14] |
王晨. 基于人工神经网络的空气颗粒物浓度预测模型[D]. 杭州: 浙江工业大学, 2018.
|
| [15] |
赵文芳, 林润生, 唐伟, 等. 基于深度学习的PM2.5短期预测模型[J]. 南京师大学报(自然科学版), 2019, 42(3): 32-41. |
| [16] |
CLAPP L J, JENKIN M E. Analysis of the relationship between ambient levels of O3, NO2 and NO as a function of NOx in the UK[J]. Atmospheric Environment, 2001, 35(36): 6391-6405. |
| [17] |
STEPHENS S, MADRONICH S, WU F, et al. Weekly patterns of Mexico City's surface concentrations of CO, NOx, PM10 and O3 during 1986—2007[J]. Atmospheric Chemistry and Physics, 2008, 8(17): 5313-5325. |
| [18] |
CHEUNG V, WANG T. Observational study of ozone pollution at a rural site in the Yangtze Delta of China[J]. Atmospheric Environment, 2001, 35(29): 4947-4958. |
| [19] |
王占山, 李云婷, 陈添, 等. 北京城区臭氧日变化特征及与前体物的相关性分析[J]. 中国环境科学, 2014, 34(12): 3001-3008. |
| [20] |
吴慧静, 赫晓慧. 基于GA-BP神经网络的空气质量指数预测研究[J]. 安徽师范大学学报(自然科学版), 2019, 42(4): 360-365. |
| [21] |
王子瑞. 沈阳市空气质量指数(AQI)时间变化特征分析及预测模型比较研究[D]. 沈阳: 沈阳农业大学, 2020.
|
| [22] |
生态环境部. 环境空气质量数值预报技术规范: HJ 1130—2020[S]. 北京: 中国环境科学出版社, 2020.
|
| [23] |
WILLMOTT C J. On the validation of models[J]. Physical Geography, 1981, 2(55): 184-194. |
| [24] |
张旭. 基于神经网络的空气质量预测[D]. 南京: 南京信息工程大学, 2019.
|
 2023, Vol. 15
2023, Vol. 15 

