2. 河北东方学院, 河北 廊坊 065000
2. Hebei Oriental University, Langfang, Hebei 065000, China
京津冀地区人口较为密集,经济也比较发达,是目前我国北方地区最具经济活力的一个城市集群[1]。随着经济的快速发展,京津冀地区的空气污染问题也越来越严峻,引起了社会与政府的广泛关注。空气污染具有空间溢出性,某一地区的空气污染不仅与当地的能源消耗结构、经济结构、居民生活、交通结构等息息相关,而且还会受到附近区域的影响。
近年来,国内外学者多运用空间计量经济学、多元统计、莫兰指数(Moran's I)及灰色关联模型等[2-3]对我国城市集群的空气污染与空间关联问题进行研究。2014年,国家提出了京津冀协同发展战略。自此以后,国内外学者对京津冀地区的生态环境与协同发展问题进行了大量的研究。一些学者对京津冀地区的能源结构与能源消耗问题进行了研究,并对其与空气污染的关联性进行了分析[4-5];部分学者对京津冀地区空气污染的空间关联进行了统计分析,对其时空演化进行了系统论述,发现该地区不同城市的空气污染具有较强的空间溢出效应[6-10]。在研究方法方面,国内学者也进行了一定的创新。基于复杂网络理论,马宇博等[11]对京津冀雾霾污染网络进行了统计分析。基于权重综合指数,乔建刚等[12]对京津冀地区不同污染物的重要性进行了排序。基于GIS空间技术和统计学方法,李慧杰等[13]对京津冀地区空气污染的影响因素进行了分析。
“21世纪将是复杂性科学的世纪”,这是世界著名物理学家霍金对于复杂性科学的精彩论述。复杂网络是复杂性科学的核心内容,自从复杂网络的无标度特征和小世界性被提出以后[14-15],国内外掀起了研究复杂网络的热潮。当前,复杂网络的研究成果多集中于自然科学[16]、物理科学[17]、管理科学[18]、社会经济学[19-20]等领域。在生态环境领域,虽然有部分学者运用复杂网络理论对城市空气质量空间关联与演化进行了相应的研究,但是从模体[21]视角出发对城市空气污染空间关联及其协同治理进行的探讨还鲜有涉及。
为了探求京津冀及周边城市空气污染的空间关联、季节演化情况及模体视角下的城市环境协同治理,本研究于2015年1月1日至2021年12月31日,选取京津冀及周边共31个城市的空气质量指数(AQI)日均值作为样本,通过计算不同城市AQI的皮尔逊相关系数,结合引力模型,构建京津冀及周边城市的空气污染关联网络,并对网络的整体特征与季节演化情况进行了分析;构建了春、夏、秋、冬4个季节的模体关联网络图,对模体A及模体B随季节演化情况进行了分析,并基于模体演化情况,对京津冀及周边城市的环境协同治理提出了相应的对策与建议。
1 数据来源与研究方法 1.1 数据来源 1.1.1 AQI日均值2015年1月1日至2021年12月31日京津冀及周边31个城市的AQI日均值从中国空气质量在线检测平台(https://www.aqistudy.cn/historydata/)获取。31个城市包括北京、石家庄、天津、唐山、沧州、廊坊、邯郸、邢台、秦皇岛、保定、衡水、郑州、濮阳、鹤壁、安阳、焦作、开封、新乡、晋城、朔州、大同、晋中、忻州、济南、德州、长治、承德、太原、阳泉、张家口、聊城。
1.1.2 城市空间距离2个城市之间的空间直线距离利用Python软件通过经纬度计算获取。
1.2 研究方法 1.2.1 空气质量空间关联网络的建立为了使用复杂网络可视化软件Gephi构建一个较为健壮的空气质量空间关联复杂网络,首先应用SPSS软件计算出31个城市中任意2个城市的皮尔逊相关系数,构建了一个31×31的相关矩阵。参考马宇博[22]研究中的使用方法,以所有相关系数的平均值作为阈值,如果2个城市之间的相关系数大于阈值,则2个城市之间存在1条边,如果2个城市之间的相关系数小于阈值,则边不存在。对于2个城市之间的边的权重,除了考虑相关系数外,还应当考虑空间距离。权重由于受到量纲的影响,差异较大,需要进行归一化处理。
1.2.2 关联网络节点的度与中心性度是度量网络中节点重要性的最重要的指标。在无向网络中,度表示与这个节点直接相连的节点的数目。在构建的京津冀及周边城市空气质量空间关联网络中,如果1个节点度值越高,代表与这个城市节点空气质量存在空间关联的城市数量越多。节点的度的计算公式见式(1)。
| $k_i=\sum _{j \in V} m_{i j} $ | (1) |
式中:ki——节点名称为i的度值;i和j——任意节点,对应文中表示城市;V——节点集合;mij——节点i和j之间是否存在连边,若存在连边,则mij记为1,否则记为0。
度量节点重要性的指标除了度以外,还有中介中心性与接近中心性。
中介中心性[23]是度量网络中的某个节点的中心性的重要指标,代表该节点在多大程度上位于网络图中其他节点对的中间位置。如果1个节点处于多对节点对之间,那么该节点的度值一般比较低,但这个节点可能在网络连接中起到重要的“中介作用”。中介中心性的计算公式见式(2)。
| $ \mathrm{BE}_i=\sum _{s, r \neq i} \frac{d_{s r}(i)}{d_{s r}} $ | (2) |
式中:BEi——节点i的中介中心性;dsr(i)——节点s到r的最短路径中经过i节点的数量;dsr——节点s到r的最短路径数量。
接近中心性[24]也是度量节点重要性的重要指标,一般用来度量网络中的某个节点到其他节点的最短路径的平均长度。即在复杂网络中,如果1个节点离其他节点距离越近,那么它的接近中心性就越高。接近中心性的计算公式见式(3)。
| $\mathrm{CL}_i=\frac{n-1}{\sum _{j \neq i} d_{i j}} $ | (3) |
式中:CLi——节点i的接近中心性;n——节点数量;dij——节点i与j之间的最短距离。
1.2.3 季节关联网络及其模体演化分析为了清晰地展示京津冀及周边城市空气污染空间关联随季节演化的情况,构建了31个城市的空气质量空间关联四季网络图,并对网络图的度、平均度、网络密度及关键城市关联情况进行分析。为了揭示4个季节关联网络的构建模式,引入了“模体”的概念,使用fanmod软件对四季关联网络中反复出现的局部结构进行统计分析,探究了季节关联网络模体的存在情况及其演化特征。
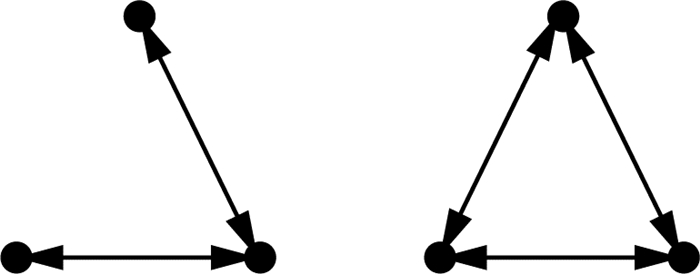
模体是1种特殊的网络结构,通常由少数节点组成,是在复杂网络中出现多次的具有同样结构的网络子图。复杂网络分为有向图与无向图,在有向图中,如果模体由3个节点构成,共包含13种网络结构;如果模体由4个节点构成,共包含199种网络结构。无向图中的模体结构则较为简单,由3个节点构成的模体只包含2种网络结构,见图 1。
|
图 1 无向图中3个节点的模体示意 |
在复杂网络中,模体的频率是指该模体在复杂网络中出现的次数,计算公式见式(4)。
| $f(V)=\frac{n(V)}{N} $ | (4) |
式中:f(V)——模体V在网络中出现的次数,即频率;n(V)——由n个节点组成的模体V在网络中存在的次数;N——1个网络中所有的由n个节点组成的模体出现的总次数。
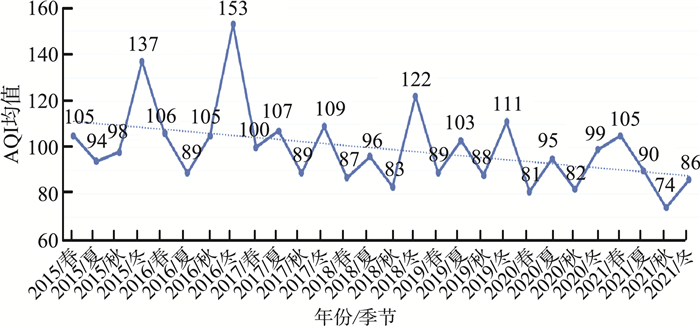
2 结果与分析 2.1 31个城市空气质量分布特征 2.1.1 31个城市AQI时间变化特征2015—2021年京津冀及周边31个城市AQI季度均值时序变化见图 2。由图 2可见,AQI总体上呈下降趋势,说明各个城市整体环境质量有所改善。从季节上看,冬季的AQI均值最大,随着气温上升,AQI均值逐渐呈现下降趋势,并在夏季或秋季达到最低值。之后随着温度下降,AQI值又逐渐呈现上升趋势,并在冬季达到最高值。不同季节的AQI均值对应的空气质量等级大部分集中在良(AQI值为50~100),说明2015—2021年该区域大气环境质量得到显著改善。呈现这种变化规律的原因可能是该区域冬季气温低,空气流通速度慢,不利于大气污染物扩散,而夏季气温高,降雨量大,秋季冷暖空气对流速度快,有利于污染物的沉降和扩散[25]。
|
图 2 2015—2021年京津冀及周边31个城市AQI季度均值时序变化 |
2015—2021年京津冀及周边31个城市AQI年均值变化见图 3。由图 3可见,空气质量整体呈现出北部区域较好,南部区域较差的现象。将31个城市按照AQI年均值分为3类:以承德、张家口、大同、秦皇岛为代表的北部地区,AQI年均值<80,对应空气质量等级为良,空气质量相对较好;以北京、天津、晋城、长治、晋中、阳泉、沧州、忻州、朔州为代表的中部地区,AQI年均值为80~100,空气质量水平居中;以保定、石家庄、衡水、德州、邢台、邯郸、聊城、安阳为代表的南部地区,AQI年均值>100,对应空气质量等级为轻度污染,空气质量相对较差。这可能是因为北部地区重工业较少,污染物排放量较低,且北部地形较高,处于上风向,有利于大气污染物的扩散;而中部和南部地区重工业较多,污染物排放量较高,且中南部地形较低,处于下风向,不利于大气中污染物的扩散[25]。

|
图 3 2015—2021年京津冀及周边31个城市AQI年均值变化 |
对城市AQI数据进行正态分布检验,发现总体符合正态分布特征,因此选用皮尔逊相关系数进行分析。选取31个城市的AQI日均值进行二元分析,得到城市之间的相关系数。2015—2021年京津冀及周边31个城市皮尔逊相关系数热力图见图 4(横、纵坐标的城市排名按照纬度自北向南依次排列)。由图 4可见,右下角区域颜色相对较深,表明这些城市之间的相关性较大。这一现象与各城市之间地域距离存在较大关联。以衡水、德州、邢台、邯郸等为代表的南部区域的相关性强于北部区域,说明空气污染比较严重的城市之间的关联性较强,溢出效应也较高,这一现象与区域间的空气流通和大气污染物的扩散密不可分。

|
图 4 2015—2021年京津冀及周边31个城市皮尔逊相关系数热力图 |
以31个城市为节点,城市之间的关联关系为边,以城市相关系数与对应城市间的平均距离的比值为边的权重,以31个城市间的皮尔逊相关系数的均值为阈值(经计算均值为0.547 9)。由此,构建出了包含31个节点与231条边的空气污染空间关联网络。
2.3.1 空气污染空间关联网络特征与度分布2015—2021年京津冀及周边31个城市空气污染空间关联社会网络示意见图 5。此网络平均度值为14.903,网络密度为0.497,表明京津冀及周边城市空气污染空间关联网较为紧密。由图 5可见,存在一些空气质量空间关联较为紧密的城市对,如邯郸与安阳、廊坊与北京、焦作与新乡、太原与晋中等,针对这些城市,解决空气污染问题时应尽量协同治理,制定合作共赢的方针政策。此外,在空间关联网络中,邢台与石家庄度值最高,表明这2个城市与网络中多个城市空气质量存在空间关联,空气污染具有较强的空间溢出效应。

|
图 5 2015—2021年京津冀及周边31个城市空气污染空间关联社会网络示意 |
2015—2021年京津冀及周边31个城市度值排序见表 1。由表 1可见,邢台、石家庄、邯郸、保定、衡水为度值最高的5座城市,这些城市度值均≥20,表明与其他城市空气质量关联较为紧密,在空气污染方面有较强的传播力和影响力。节点度值最低的城市是张家口,与其他城市相比,张家口全年空气质量较好,与其他城市的空间关联也较弱。
| 表 1 2015—2021年京津冀及周边31个城市度值排序 |
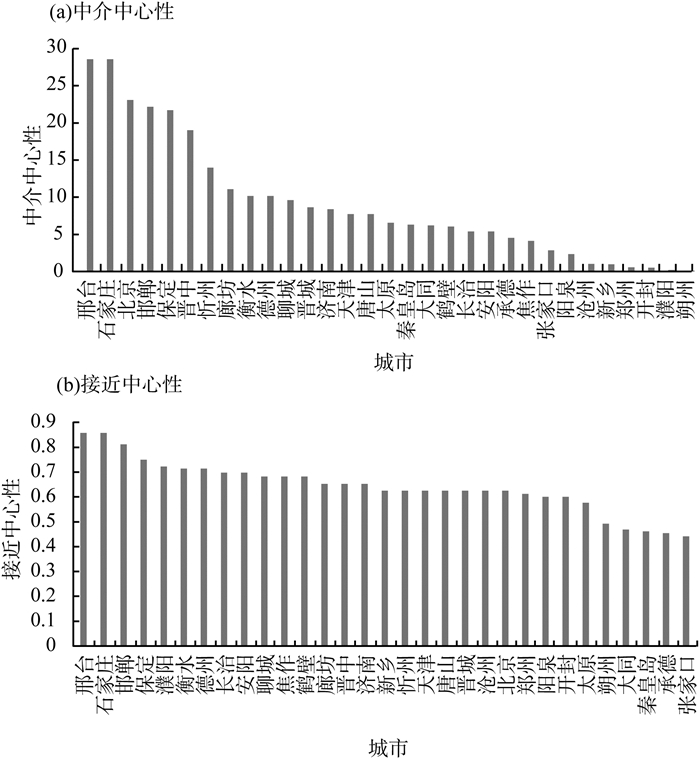
2015—2021年京津冀及周边31个城市的中介中心性与接近中心性见图 6(a)(b)。由图 6可见,中介中心性排名前5位的城市分别是邢台、石家庄、北京、邯郸及保定,这些城市的媒介作用较强,对其他城市有较大的溢出效应。相比于中介中心性,接近中心性在几何地理上更接近中心位置。接近中心性排名前3位的城市分别是邢台、石家庄及邯郸,这些城市距离其他城市的路径之和最短,一旦这些城市的空气受到严重污染,周边较大范围地区的空气质量也将在一定程度上受到负面影响。由上述研究可知,邢台、石家庄及邯郸这3个城市的中介中心性与接近中心性排名均靠前,说明它们处于网络中的核心位置,空气污染传播的能力最强。
|
图 6 2015—2021年京津冀及周边31个城市的中介中心性与接近中心性 |
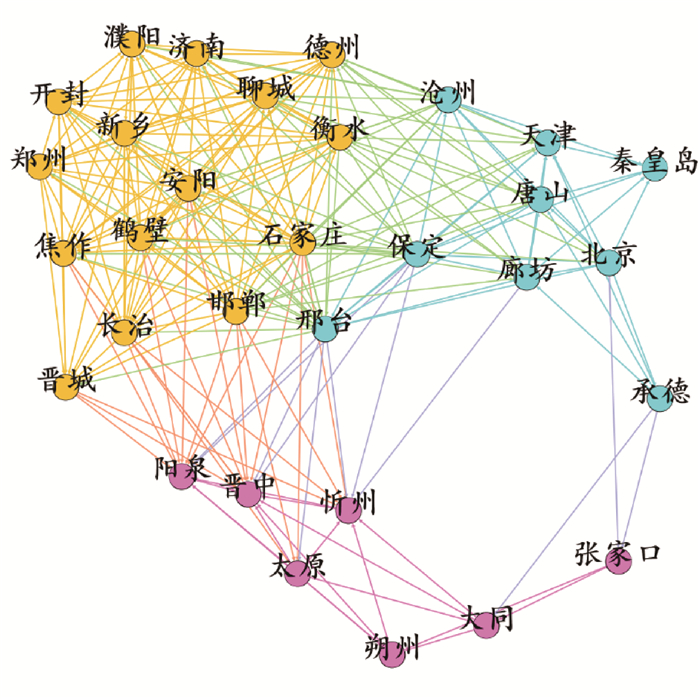
基于Gephi软件对网络图进行模块化处理,2015—2021年京津冀及周边31个城市模块化与子群展示示意见图 7。由图 7可见,京津冀及周边城市空气污染空间关联网络共分为3个凝集子群,石家庄、邢台及邯郸处于3个子群发生关联的中心位置,再次验证了上述结论。
|
图 7 2015—2021年京津冀及周边31个城市模块化与子群展示示意 |
为了探究季节对城市空气污染空间关联的影响,对原始数据按照气温划分季节,春季为3、4、5月份,夏季为6、7、8月份,秋季为9、10、11月份,冬季为12、1、2月份。通过对4个季节的空间网络图的图密度和度值进行统计计算,可知春季图密度为0.531,平均度值为15.935;夏季图密度为0.484,平均度值为14.516;秋季图密度为0.471,平均度值为14.129;冬季图密度为0.477,平均度值为14.323。可见4个季节的空气污染空间关联网络图差异不大,密度与平均度值均较高,不同城市之间的AQI关联较为紧密,春季网络密度最高,这可能与北方春季多大风天气有关。
通过对4个季节的关联网络图的模体进行统计分析,发现每个季节中均存在2个模体,模体A为3个节点两两关联的模体,模体B为3个节点中2个节点存在关联的模体。边代表 2个节点城市间存在关联关系,权重表示2个节点间存在关联程度的大小。2015—2021年京津冀及周边31个城市4个季节模体演化网络图见图 8(a)—(h)。由图 8可见,从整体来看,模体A网络图节点间的关联程度比模体B的更紧密。

|
图 8 2015—2021年京津冀及周边31个城市4个季节模体演化网络图 |
由图 8(a)—(d)可见,4个季节均以石家庄、邢台和邯郸为主要传播城市,其中春季模体关联密度明显高于其他3个季节,该网络的平均度值为13.2,平均加权度值为56.933。由图 8(e)—(h)可见,4个季节主要以邯郸和北京为枢纽城市,表明邯郸和北京在31个城市间空气污染的传播过程中起着重要作用,在治理中需要重点防控。春季模体的关联程度略高于其他3个季节,不同的网络中同一类模体的频率不同,模体频率越高,说明该模体在真实网络中出现的次数越多,该模体也越重要。4个季节模体B的出现频率为34%~38%,其中夏季和冬季较高,均>37%,说明夏、冬两季城市之间的空气污染散播与关联程度高于春、秋两季。
3 结论与建议 3.1 结论基于复杂网络,从京津冀及周边31个城市AQI的时间变化特征和空间分布特征的角度,构建了2015—2021年该区域的空气质量空间关联加权网络,分析了空气污染空间关联与空间溢出的基本状况;构建了春、夏、秋、冬4个季节的空气污染空间关联网络,探究了不同季节对不同城市空气污染的空间关联差异性,并对季节网络进行了模体演化分析。得出以下结论:
(1) 通过对京津冀及周边31个城市AQI的时间变化特征和空间分布特征进行分析可知,该区域环境质量总体趋于好转,且区域内北部地区空气质量较好,南部地区空气质量较差。
(2) 通过对该区域空气质量空间网络的度值、中介中心性、接近中心性及凝集子群的比较分析可知,邢台、石家庄、邯郸、保定及衡水在空气污染方面有较强的传播力和影响力,其中邢台、石家庄及邯郸的中心性相对较高,处于网络的中心位置。网络共包括3个凝集子群,石家庄与邯郸处于子群发生关联的核心位置。
(3) 通过对该区域4个季节空间关联网络图进行统计分析可知,4个季节的网络图密度与度值均较高,不同城市之间的AQI关联较为紧密。在不同季节,城市之间关联的紧密程度随着季节演变发生变化,春季网络图密度最高。
(4) 通过对该区域季节关联网络模体演化特征进行分析可知,在模体A的关联网络中,石家庄、邢台、邯郸为主要传播城市;在模体B的关联网络中,邯郸和北京为枢纽城市,邯郸和北京在31个城市间空气污染的传播过程中起着重要作用。
3.2 建议对京津冀及周边城市空气污染的治理,应在该区域制定协同治理对策,建议如下:
(1) 石家庄、邢台及邯郸处于3个凝集子群中心位置,污染传播能力最强,应加强对这3个城市的治理。地方政府须完善监督管理机制,发展环保产业,走可持续发展道路。
(2) 依据当地不同的季节气候条件,制定不同的空气污染防治政策。冬季采用煤改电、煤改气、地热能等多种清洁取暖方式,实行区域或集中采暖供热,充分提高锅炉或天然气利用率,降低燃料消耗和烟尘排放量。
(3) 石家庄、邢台、邯郸、北京在模体中处于中心位置,应与其他城市开展空气污染的协同治理。从行政、法律、经济等多方面入手,为解决京津冀大气污染问题提供充分保障。
| [1] |
范凤岩, 王洪飞, 樊礼军. 京津冀地区空气污染的健康经济损失评估[J]. 生态经济, 2019, 35(9): 157-163. |
| [2] |
杨新平, 徐登国. 基于中小城市空气污染指标的时间序列模型构建[J]. 环境污染与防治, 2014, 36(11): 111. |
| [3] |
刘晓红, 江可申. 中国城市PM2.5的时空分异及影响因素分析——基于161个城市的实证研究[J]. 调研世界, 2018(1): 25-34. |
| [4] |
刘晓红, 江可申. 我国雾霾污染影响因素的空间效应——基于PM2.5的实证分析[J]. 科技管理研究, 2017, 37(12): 247-252. |
| [5] |
孟雪, 狄乾斌, 季建文. 京津冀城市群生态绩效水平测度及影响因素[J]. 经济地理, 2020, 40(1): 181-186, 225. |
| [6] |
买超平, 连素琴, 牛叔文, 等. 甘肃省能源消费结构与空气质量变化的相关性分析[J]. 兰州大学学报(自然科学版), 2014, 50(4): 508-512. |
| [7] |
许燕婷, 刘兴诏, 王振波. 基于AQI指数的中国城市空气质量时空分布特征[J]. 广西师范大学学报(自然科学版), 2019, 37(1): 187-196. |
| [8] |
程钰, 刘婷婷, 赵云璐, 等. 京津冀及周边地区"2+26"城市空气质量时空演变与经济社会驱动机理[J]. 经济地理, 2019, 39(10): 183-192. |
| [9] |
彭玏, 赵媛媛, 赵吉麟, 等. 京津冀大气污染传输通道区大气污染时空格局研究[J]. 中国环境科学, 2019, 39(2): 449-458. |
| [10] |
刘华军, 裴延峰. 经济发展与中国城市雾霾污染——基于空间关联网络情形下的考察[J]. 城市与环境研究, 2018(3): 15-41. |
| [11] |
马宇博, 高广阔. 基于节点重要性评价的京津冀雾霾污染网络研究[J]. 环境科学学报, 2018, 38(6): 2287-2296. |
| [12] |
乔建刚, 李士宣, 王英. 京津冀空气质量状况研究[J]. 应用化工, 2019, 48(11): 2791-2793. |
| [13] |
李慧杰, 王秀兰, 王计平, 等. 2013—2017年间京津冀地区空气质量及影响因素分析[J]. 环境监测管理与技术, 2019, 31(2): 21-25. |
| [14] |
WATTS D J, STROGATZ S H. Collective dynamics of smallworld networks[J]. Nature, 1998, 393(6684): 440-442. |
| [15] |
CAO Y J, WANG G Z, JIANG Q Y, et al. A neighbourhood evolving network mode[J]. Physics Letters A, 2006, 349(6): 462-466. |
| [16] |
陈刚, 王信, 肖伸平, 等. 复杂动态网络指数采样同步控制[J]. 中南大学学报(自然科学版), 2018, 49(12): 2993-3001. |
| [17] |
孔江涛, 黄健, 龚建兴, 等. 基于复杂网络动力学模型的无向加权网络节点重要性评估[J]. 物理学报, 2018, 67(9): 255-271. |
| [18] |
秦胜君. 基于复杂网络的企业创新网络级联失效可靠性模型[J]. 科技管理研究, 2017, 37(7): 199-204. |
| [19] |
樊斌锋, 杨琼. 社交复杂网络中基于无向图和聚类的社区检测关键技术研究(英文)[J]. 机床与液压, 2019, 47(12): 179-184. |
| [20] |
游鸽, 郭昊, 刘向. 复杂网络视角下的金融市场结构演化与风险传染[J]. 金融发展研究, 2020(1): 30-39. |
| [21] |
徐越, 刘雪明. 基于三元闭包模体的关键节点识别方法[J]. 复杂系统与复杂性科学, 2022, 11(2): 1-8. |
| [22] |
马宇博. 京津冀区域城市雾霾污染动态网络分析[D]. 上海: 上海理工大学, 2019.
|
| [23] |
FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41. |
| [24] |
ALEX B. Communication patterns in task-oriented groups[J]. Journal of the Acoustical Society of America, 1950, 22(6): 725-730. |
| [25] |
梁银双, 刘黎明, 卢媛. 基于函数型数据聚类的京津冀空气污染特征分析[J]. 调研世界, 2017(5): 43-48. |
 2023, Vol. 15
2023, Vol. 15 

