2. 云南省疾病预防控制中心,云南 昆明 650022;
3. 昆明市气象局,云南 昆明 650034
2. Yunnan Center for Disease Control and Prevention, Kunming, Yunnan 650022, China;
3. The Meteorological Bureau of Kunming, Kunming, Yunnan 650034, China
2017年的中国环境公报显示,近地层臭氧(O3)是6种常规观测的大气污染物中浓度不断上升的一种。昆明大气环境条件具有紫外线强度大、辐射强的特点,易导致污染物二次生成和光化学反应,造成O3浓度升高。昆明三面环山、南濒滇池,是典型的坝子地形,容易形成局地风,不利于大气污染物的扩散。
太阳辐射强度对大气光化学反应具有重要影响,大部分观测站点缺少太阳辐射数据,而气象要素中的气温、日照时数等的变化能较好地反映太阳辐射强度的变化[1]。因此,气象要素对近地层O3的影响作用不容忽视,特别是气象要素之间的交互作用对O3的产生、累积和扩散影响更加值得研究。研究表明,影响O3浓度变化最主要的气象要素是气温和日照时数,其次是相对湿度,再次是风速[2]。气温高、日照长、湿度低有利于O3生成,而地面风速的影响与特定的风向有关[2-6]。
O3浓度与气象要素之间存在非线性相互作用和滞后效应,但目前基于不同影响因素交互作用和滞后效应的非线性模型对O3浓度拟合研究并不多见。广义相加模型(GAM)是广义线性模型和可加模型的结合形式,可用于响应变量与解释变量之间的关系是非线性和非单调数据的分析,已被广泛应用于处理复杂的非线性空气污染问题[7]。很多学者[8-11]基于GAM模型,进行了细颗粒物(PM2.5)预测研究,分析了对O3浓度影响最大的气象要素。胡成媛等[12]通过构建GAM模型对四川盆地18个城市O3污染的主导气象因子进行识别,并对2017年O3浓度进行预测和检验。
基于此,对昆明坝子地形特征下O3浓度与气象要素之间的交互作用和滞后效应进行研究也十分必要。现构造了纳入滞后项和交互项的光滑回归函数,建立O3浓度变化与影响因素的非线性GAM模型。采用分布滞后非线性模型(DLNM)选取有滞后效应的高影响因子,尝试分析多种影响因素的交互作用,并归纳出多要素交互影响的典型天气形势,以期为云贵高原O3污染防治提供科学依据。
1 模型介绍 1.1 GAM模型GAM模型是一种非参数回归模型,包含参数项和非参数平滑项,无须设定参数,也不需要掌握因变量与自变量之间的关系。非参数平滑项是GAM的关键部分,自变量分成若干区间,每个区间通过解释变量函数拟合生成平稳、光滑的回归曲线。因变量的分布可以是正态分布、二项分布、泊松分布(Poisson分布)等。
GAM是在广义线性模型和可加模型的基础上发展而来的非参数模型,弥补了广义线性模型中自变量与因变量间可用函数关系有限的不足,用非参数方法来拟合有时间变化趋势的预测变量,表征自变量对因变量的贡献,具有较高的灵活性,尤其在探索性研究中可以降低建模难度,节约大量的时间[13],被广泛应用于生态学研究中。
1.2 DLNM模型DLNM模型主要研究时间序列数据的非线性和滞后性影响。首先利用交叉基函数进行特征向量转换,得到新的暴露-滞后矩阵。其次用广义线性模型对变换后的数据进行建模。
DLNM是在GAM模型与分布滞后线性模型等传统模型的基础上结合而成,核心思想是通过交叉基函数向暴露-反应关系添加滞后维度,从而同时描述其效应在自变量维度和滞后维度的变化分布[14]。
2 数据来源O3数据选用2018—2021年O3日最大8 h滑动平均值[ρ(O3-8 h)],来源于中国空气质量在线监测分析平台历史数据(https://www.aqistudy.cn/historydata/)。同期每天的气象要素数据为昆明市气象局气象站常规观测资料,包括平均气温、平均相对湿度、平均地面气压、平均日照时数、平均水汽压和平均风速。
昆明O3逐日质量浓度等级划分标准参考文献[15],划分为5个等级:低质量浓度段(1~80 μg/m3)、较低质量浓度段(81~120 μg/m3)、一般质量浓度段(121~160 μg/m3)、较高质量浓度段(161~200 μg/m3)和超标质量浓度段(>200 μg/m3)。
3 结果与分析 3.1 数据基本情况昆明市2018—2021年O3质量浓度和气象要素统计信息见表 1。由表 1可见,平均ρ(O3-8 h)为83.8 μg/m3,日平均相对湿度为68.2%。
| 表 1 昆明市2018—2021年O3质量浓度和气象要素统计信息 |
平均气温、日照时数、平均风速与ρ(O3-8 h)呈现正相关关系(相关系数分别为0.293,0.514和0.254,P<0.01);相对湿度、地面气压、水汽压与ρ(O3-8 h)呈现负相关关系(相关系数分别为-0.679,-0.222和-0.230,P<0.01)。
3.2 GAM模型的单气象要素分析选取相对湿度、平均气温、水汽压、地面气压、日照时数和平均风速作为自变量,ρ(O3-8 h)为因变量构建拟合模型。表达式见式(1)。
| $ \begin{aligned} & \log \left[\mathrm{E}\left(Y_t\right)\right]=\alpha+\mathrm{s}(\text { weather, df })+\mathrm{ns}(\text { time, df }) \\ + & \gamma \text { dow } \end{aligned} $ | (1) |
式中:E——Yt在概率意义上的数值,即预测值;Yt——第t天的ρ(O3-8 h),μg/m3;α——截距;s——非参数平滑样条函数;weather——气象要素;df——自由度;ns——自然立方样条函数;time——时间序列变量;γ——对应效应的系数;dow——星期几哑变量。排除长期趋势等混杂因素的影响。
将6个气象要素中的1个要素作为自变量,ρ(O3-8 h)为因变量,控制其他相关要素的混杂效应影响,采用平滑样条函数构建拟合模型,根据GAM模型的估计自由度、参考自由度、F检验统计量(F)、匹配显著性标记(P-value),广义交叉验证得分(GCV)、方差解释率和判定系数(R2),分析单气象要素对ρ(O3-8 h)的影响和拟合效果(表 2)。6个气象要素与ρ(O3-8 h)均在P<0.01水平下显著相关。
| 表 2 GAM模型的单气象要素对ρ(O3-8 h)的影响和拟合效果 |
由表 2可见,相对湿度和日照时数对模型的解释率较高,其他要素对模型的解释率较低。6个要素自由度均>1,表示气象要素与ρ(O3-8 h)是非线性曲线关系。
GAM模型6个气象要素与ρ(O3-8 h)的平滑曲线拟合见图 1(a)—(f),其中实线为拟合线,阴影区域为95%置信区间,水平坐标轴短线为气象要素值分布区间情况。由图 1(a)和(f)可见,拟合曲线近似直线,相对湿度与ρ(O3-8 h)负相关,当相对湿度<38%时,ρ(O3-8 h)>160 μg/m3。平均风速与ρ(O3-8 h)正相关。由图 1(b)和(e)可见,拟合曲线近似反“L”形,平均气温和日照时数与ρ(O3-8 h)正相关,当平均气温<15.6 ℃时,ρ(O3-8 h) 随平均气温升高而缓慢升高;当平均气温为15.6 ~20.5 ℃时,ρ(O3-8 h)随平均气温升高而缓慢下降;当平均气温>20.5 ℃时,ρ(O3-8 h)随平均气温升高而快速升高;当平均气温>23.5 ℃时,ρ(O3-8 h)>160 μg/m3。ρ(O3-8 h)随日照时数呈波动性升高,当日照时数>12 h时,ρ(O3-8 h)>160 μg/m3。由图 1(c)可见,拟合曲线近似倒“S”形。由图 1(d)可见,拟合曲线近似倒“U”形。地面气压和水汽压在合适的区间内,ρ(O3-8 h)较高;地面气压<809 hPa时,ρ(O3-8 h)随地面气压升高而快速升高;地面气压在为数不多的高值样本中出现ρ(O3-8 h)升高的趋势。

|
图 1 GAM模型6个气象要素与ρ(O3-8 h)的平滑曲线拟合 |
气象要素对ρ(O3-8 h)的影响可能有持续性,O3的积累不但与当日气象要素有关,而且还可能与前几天的气象要素状况有关,O3的形成有滞后性,采用DLNM模型分析其滞后性。表达式见式(2)。
| $ \begin{aligned} & \log \left[\mathrm{E}\left(Y_t\right)\right]=\alpha+\operatorname{cb}(\text { weather }, \beta)+\mathrm{ns}(\text { time, } \\ & \text { df })+\gamma \text { dow } \end{aligned} $ | (2) |
式中:cb——交叉基矩阵;β——滞后期;E、Yt、α、weather、ns、time、df、γ、dow同式(1)。排除长期趋势等混杂因素的影响。
采用相对危险度(RR)分析气象要素对ρ(O3-8 h) 的总体效应和滞后期,结果见图 2(a)—(d)。由图 2(a)(b)可见,地面气压>820 hPa、平均风速<2.1 m/s时,对ρ(O3-8 h)总体效应的RR值>1.0,且均具有统计学意义(P<0.05),并且在地面气压为821 hPa和平均风速为0.6 m/s时RR值达到峰值,分别为1.86(95%置信区间:1.15~2.99)和2.26(95%置信区间:1.91~2.68)。由图 2(c)(d)可见,地面气压>818 hPa、平均风速<2.0 m/s,滞后1~3 d时,ρ(O3-8 h)有升高的趋势(RR值>1.0)。
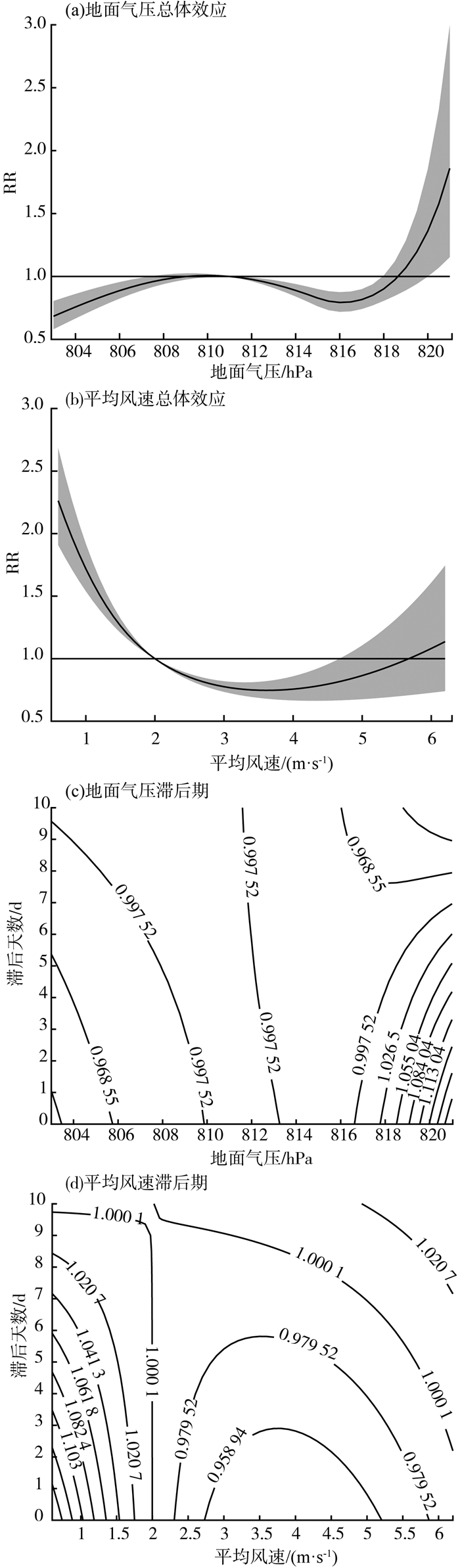
|
图 2 气象要素对ρ(O3-8 h)的总体效应和滞后期 注:(c)和(d)为RR等值线分析。 |
气象要素之间存在交互作用,将有物理意义的交互项纳入模型,采用若干组2个连续自变量的交互项的平滑回归函数和单自变量的非参数平滑样条函数(包含滞后项的自变量平滑函数)与ρ(O3-8 h)的关系建立GAM模型,表达式见式(3)。
| $ \log \left[\mathrm{E}\left(Y_t\right)\right]=\alpha+\mathrm{s}(\text { weather, df })+\text { te }\left(\text { weather }_i\right. \text {, } \\ \text {weather} \left._j, \mathrm{df}\right)+\mathrm{ns}(\text { time, df} )+\gamma \text {dow} $ | (3) |
式中:te——weatheri和weatherj 2种气象要素交互项的平滑回归函数;E、Yt、α、s、weather、df、ns、time、γ、dow同式(1)。相对湿度、平均气温、水汽压、地面气压、日照时数和平均风速分别用rhum、temp、q、p、h、w表示,滞后时间用正整数表示,如p1表示1 d前的地面气压,以此类推。滞后项和交互项GAM模型的多气象要素分析见表 3。
| 表 3 滞后项和交互项GAM模型的多气象要素分析 |
由表 3可见,12个交互项的P-value均<0.05,故对ρ(O3-8 h)的拟合有显著影响。模型中交互项涵盖当天的相对湿度、平均气温、水汽压、地面气压、日照时数和平均风速,前1 d的相对湿度、平均气温、地面气压和平均风速,前2 d的地面气压和平均风速。
分别用单要素项和多要素交互项建立GAM模型。单要素项(s为单要素平滑样条函数)和2个要素交互项(te为交互项的平滑回归函数)的GAM模型的效果检验见表 4。
| 表 4 单要素项和2个要素交互项的GAM模型的效果检验 |
由表 4可见,s函数模型和te函数模型的R2均>0.6,方差解释率均>60%,GCV均<390,表明模型拟合效果较好。相对而言,te函数模型优于s函数模型。
3.5 气象要素交互项作用分析各气象要素交互项对ρ(O3-8 h)的影响效应见图 3(a)—(c)。由图 3(a)可见,平均气温为13~23 ℃、水汽压为9~19 hPa时,对ρ(O3-8 h)的影响较高,适当的气温和适中的水汽压有利于ρ(O3-8 h)的增加。由图 3(b)可见,平均气温<20 ℃、相对湿度<60%时,与平均气温>20 ℃、相对湿度>80%相比,对ρ(O3-8 h)的影响较大,干冷和湿热天气有利于ρ(O3-8 h)的增加。由图 3(c)可见,平均风速<2.5 m/s、地面气压>815 hPa时,与平均风速>3.0 m/s、地面气压<808 hPa相比,对ρ(O3-8 h)的影响较大,低压大风和高压小风天气有利于ρ(O3-8 h)的聚集增加。

|
图 3 各气象要素交互项对ρ(O3-8 h)的影响效应 |
通常地面风速较小有利于O3的生成和累积,风速较大有利于O3的扩散。但是风速较大一方面易于扩散本地O3,另一方面易于输送生成源O3到本地。在O3区域传输中,风速的作用有着复杂多变的特征,主要是地面天气形势(气压场)的背景下风速和O3生成源的对应关系。在O3污染最多的春季,昆明的对流层低层以西风环流为主,不仅中南半岛地区(东南亚)生物体燃烧会对昆明地区对流层低层O3浓度有影响,而且南亚地区(印度中部、中南半岛西部临近孟加拉湾地区)的生物体燃烧也对昆明地区有影响[16]。
为了进一步阐明地面气压场与地面风速对O3浓度交互影响的关系,统计2018—2021年昆明ρ(O3-8 h)的实测值,发现较高质量浓度等级(161~200 μg/m3)共出现20 d,分析每个个例的天气形势,有10 d为高压系统,6 d为低压系统,4 d为其他类型系统。低压系统的平均风速为3.0 m/s,高压系统的平均风速为1.5 m/s。绘制6 d低压系统和10 d高压系统的平均海平面气压形势场,见图 4(a)(b)。

|
图 4 2种类型平均海平面气压形势场 注:黑灰添色为海拔高度(m),白色实线为海平面气压(hPa),蓝色箭头为地面风速(m/s),图底部为风速标尺。 |
由图 4(a)可见,低压大风,通常是空气辐合,周边O3的聚集增加;图 4(b)是高压小风,一般是晴热天气,太阳辐射强,利于O3生成,而且局部O3扩散速度较慢,易在大气低层积累。
3.6 机器学习模型与GAM模型比较对比交互项(包含滞后项)的GAM模型与其他的机器学习模型[17-18],如支持向量机(SVM)和长短期记忆网络(LSTM)的拟合效果,按照划分的5个等级标准评判准确率,对2018—2021年昆明市每天的ρ(O3-8 h)进行拟合,使用绝对误差、标准偏差和5个等级标准拟合准确率指标,以检验拟合效果。机器学习模型与GAM模型的ρ(O3-8 h)拟合效果比较见表 5。
| 表 5 机器学习模型与GAM模型的ρ(O3-8 h)拟合效果比较 |
由表 5可见,交互项GAM模型的绝对误差值最低,拟合准确率最高。标准偏差反映数值相对于平均值的离散程度。一般的机器学习模型拟合结果主要对较大值和较小值的拟合误差较大,拟合曲线趋向平均值,峰值和谷值很难接近,交互项GAM模型的标准偏差为29.2 μg/m3,大于其他模型。因此,交互项(包含滞后项)的GAM模型的拟合效果好于其他模型。
4 结论构造了纳入滞后项和交互项的光滑回归函数,建立O3浓度变化与影响因素的非线性GAM模型。采用DLNM模型选取有滞后效应的高影响因子,尝试检验多种影响因素的交互作用,并归纳出多要素交互影响的典型天气形势,研究了昆明坝子地形特征下O3浓度与气象要素之间的交互作用和滞后效应。
(1) 平均气温和日照时数与ρ(O3-8 h)正相关,相对湿度与ρ(O3-8 h)负相关。ρ(O3-8 h)随平均气温、日照时数呈波动性升高。高气温(>23.5 ℃)、长日照时数(>12 h)、低相对湿度(<38%)等气象要素有利于局部O3的生成和累积,产生一般质量浓度段(>160 μg/m3)的O3。综合分析发现,地面气压、平均风速和水汽压在合适的区间内,ρ(O3-8 h)较高。
(2) 采用DLNM模型分析,表明地面气压和平均风速滞后1~3 d,滞后项与ρ(O3-8 h)的关联较高。
(3) 用GAM模型的单要素项对ρ(O3-8 h)进行拟合发现,单要素平滑样条函数没有显著性影响,纳入交互项后,交互项的平滑回归函数对ρ(O3-8 h)变化有显著性影响。
(4) 风速的区域传输作用比较复杂,分析地面天气形势的背景,才能发现风速和ρ(O3-8 h)的变化关系。O3高质量浓度等级的天气形势最常见有2类:首先是低压大风类,特点是空气辐合,O3聚集;其次是高压小风类,特点是晴热天气,太阳辐射强,利于O3生成,而且局部O3扩散速度较慢,易在大气低层积累。
(5) 纳入交互项(包含滞后项)的GAM模型与其他机器学习模型进行比较,交互项GAM模型的拟合误差小、准确率高,特别在拟合因变量峰值和谷值优势明显。交互项(包含滞后项)的GAM模型的拟合效果好于其他模型。
| [1] |
严文莲, 刘端阳, 康志明, 等. 江苏臭氧污染特征及其与气象因子的关系[J]. 气象科学, 2019, 39(4): 477-487. |
| [2] |
严晓瑜, 缑晓辉, 杨婧, 等. 中国典型城市臭氧变化特征及其与气象条件的关系[J]. 高原气象, 2020, 39(2): 206-220. |
| [3] |
杨雪, 秦玮, 王晨波, 等. 江苏省春季臭氧污染特征分析[J]. 环境监控与预警, 2021, 13(1): 20-24. |
| [4] |
史霖. 银川市臭氧浓度与气象要素的相关性及其预测方法研究[J]. 环境科学与管理, 2020, 45(4): 125-128. |
| [5] |
陈辰, 洪莹莹, 谭浩波, 等. 佛山臭氧浓度预报方程的建立与应用[J]. 环境科学, 2022, 43(10): 4316-4326. |
| [6] |
庞业, 潘润西, 何宇, 等. 广西臭氧时空分布特征及污染天气类型研究[J]. 环境监控与预警, 2019, 11(3): 44-48. |
| [7] |
许亦频, 倪苹. 适用于大数据集的广义可加模型[J]. 统计研究, 2016, 33(4): 104-112. |
| [8] |
李莉莉, 张璇, 杜梅慧. 基于广义可加模型的PM2.5预测研究[J]. 数理统计与管理, 2020, 39(5): 811-823. |
| [9] |
黄小刚, 邵天杰, 赵景波, 等. 基于GAM模型的西安市O3浓度影响因素解析[J]. 环境科学, 2020, 41(4): 1535-1543. |
| [10] |
任至涵, 倪长健, 花瑞阳, 等. 成都O3逐日污染潜势关键时段优选的GAM模型[J]. 中国环境科学, 2021, 41(11): 5079-5085. |
| [11] |
张莹, 倪长健, 冯鑫媛, 等. 基于GAMs模型分析成都市气象因子交互作用对O3浓度变化的影响[J]. 环境科学, 2021, 42(11): 5228-5238. |
| [12] |
胡成媛, 康平, 吴锴, 等. 基于GAM模型的四川盆地臭氧时空分布特征及影响因素研究[J]. 环境科学学报, 2019, 39(3): 809-820. |
| [13] |
王彤, 贾彬, 王琳娜. 广义可加模型稳健估计在空气污染对健康影响评价中的应用[J]. 中国卫生统计, 2007, 24(3): 245-247. |
| [14] |
杨军, 欧春泉, 丁研, 等. 分布滞后非线性模型[J]. 中国卫生统计, 2012, 29(5): 772-773. |
| [15] |
洪盛茂, 焦荔, 何曦, 等. 杭州市区大气臭氧浓度变化及气象要素影响[J]. 应用气象学报, 2009, 20(5): 602-611. |
| [16] |
郑永光, 陈炯, 朱佩君, 等. 南亚地区生物体燃烧对昆明地区对流层中下层臭氧浓度的影响[J]. 北京大学学报(自然科学版), 2006, 43(3): 12-18. |
| [17] |
铁治欣, 程晓宁, 林德守, 等. 基于时间序列延迟相关算法改进LSTM的臭氧浓度预测模型[J]. 软件工程与应用, 2020, 9(2): 135-142. |
| [18] |
董红召. 融合时空特征的PCA-PSO-SVM臭氧(O3)预测方法研究[J]. 中国环境科学, 2021, 41(2): 596-605. |
 2023, Vol. 15
2023, Vol. 15 

