2. 哈尔滨市疾病预防控制中心,黑龙江 哈尔滨 150030;
3. 暨南大学疾病预防控制研究院,广东 广州 510632
2. Harbin Center for Disease Control and Prevention, Harbin, Heilongjiang 150030, China;
3. Disease Control and Prevention Institute, Jinan University, Guangzhou, Guangdong 510632, China
细颗粒物(PM2.5)即空气动力学直径≤2.5 μm的颗粒,已被证实可增加人群死亡和发病风险[1],每年导致全球310万人过早死亡,占全球疾病负担的3.2% [2]。大气PM2.5的组成成分复杂,包括元素碳、有机碳化合物、硫酸盐以及金属等[3]。流行病学研究表明,PM 2.5中的多种金属成分可通过干扰内分泌从而增加糖尿病和心血管疾病的发病风险[4]。针对中国60个城市的一项研究表明,接触PM2.5中有毒金属而导致的每例因肺癌死亡的潜在寿命损失年为19.8年[5]。然而,由于PM2.5金属化学测定相对复杂、耗时且昂贵,我国缺乏PM2.5中金属的长期监测,关于PM2.5中金属暴露对人群的健康影响研究较少。因此,亟需简单、经济、有效、准确的统计方法估算大气PM2.5中金属浓度,从而深入研究PM2.5中金属暴露对人群健康的影响,为国家进一步修订环境空气质量标准提供数据基础。
近年来,人工神经网络(BP-ANN)、支持向量机(SVM)和随机森林(RF)等机器学习方法逐渐发展且应用广泛,它们在处理复杂的非线性问题方面显示出明显优势,可用来对大气污染物进行预测[6]。Li等[7]利用RF预测中国二氧化硫(SO2)的历史浓度值;Shams等[8]应用BP-ANN预测每日二氧化氮(NO2)浓度值;Yeganeh等[9]应用SVM预测一氧化碳(CO)浓度值。相比较数值预测模型,机器学习模型中必要的输入变量更容易获取[10]。Leng等[11]将大气污染物和气象因子作为输入变量预测南京地区PM2.5中金属浓度,对比多元线性回归(MLR)、SVM和BP-ANN 3种方法后,发现SVM预测效果最优。但SVM核函数及内部参数比较依赖使用者的调参技巧,不利于模型的推广。相较于SVM模型,RF具有学习速度快、分类效果准确和防止过拟合等特点,同时能克服协变量之间复杂的交互作用[12]。然而,目前极少学者开展RF与其他机器学习方法对大气PM2.5中金属浓度预测的比对研究以及模型的评价与改善。
为寻找具有最好预测效能的算法,现以中国北方城市哈尔滨市为例,基于MLR、BP-ANN、SVM和RF算法建立大气PM2.5中多种金属污染物日均浓度的预测模型,并进行预测效能比较,寻找出最适合的大气PM2.5中金属污染物预测模型,为深入研究PM2.5中金属暴露对人群健康的影响提供技术基础。
1 研究方法 1.1 数据来源2013—2018年哈尔滨市每日气象数据(温度、湿度、气压、风速、光照和日照时间)从中国气象数据网(http://data.cma.cn/)收集。哈尔滨市12个空气质量监测站的每日大气污染物数据[NO2、SO2、CO、可吸入颗粒物(PM10)和PM2.5]从中国环境监测总站(https://www.cnemc.cn/)获取。
1.2 大气PM2.5样品采集及其金属元素测定在哈尔滨市的A区某街道和B区某街道各设置1个大气PM2.5采样点,使用PM2.5采样器(HY - 100,青岛恒远科技发展有限公司)采集大气PM2.5样品。于2013年11月—2018年12月采集样本,每月采集至少7 d,共采集样品1 118份(A区558份,B区560份)。所有样品通过修正的欧洲共同体参考物机构(BCR)提取法提取金属元素,利用电感耦合等离子体原子发射光谱仪(350D,美国珀金埃尔默股份有限公司)测定金属元素锑(Sb)、砷(As)、铅(Pb)、镉(Cd)、铊(Tl)质量浓度[13]。
1.3 模型研究方法将数据集随机分为75%的训练集和25%的测试集,采用归一化方法将数据转换为取值范围为0~1的新数据集,以消除由于指标量纲不同造成的影响。
1.3.1 MLR模型MLR模型主要建立因变量对多个自变量的多元线性回归方程,通过评估不同自变量对因变量影响的相对程度,其基本思想是找出最能代表自变量与因变量之间关系的数学表达式[14]。表达式如下:
| $ Y=\beta_0+\beta_1 X_1+\beta_2 X_2+\cdots+\beta_m X_m+e $ | (1) |
式中:β0——截距;β1,β2,…,βm——偏回归系数;e——去除m个自变量对Y影响的随机误差,又称残差;因变量Y可以近似地表示为自变量X1,X2,…,Xm的线性函数。对多元线性回归模型参数β1,β2,…,βm估计主要由最小二乘法得到,使其残差平方和最小。
1.3.2 BP-ANN模型BP-ANN是一种按照误差逆向传播算法训练的多层前馈神经网络,其基本思想是利用梯度搜索技术,以期使网络的实际输出值和期望输出值的均方误差最小[15]。BP-ANN包括输入层、隐含层和输出层,其中输入层和输出层的节点个数是确定的,而隐含层节点个数需要研究者确定。计算公式如下:
| $ h=\sqrt{m+n}+\alpha $ | (2) |
式中:h——隐含层节点数目;m——输入层节点数目;n——输出层节点数目,α——1~10之间的调节常数。
本研究根据公式(2)计算隐藏层节点数目的范围为5~14。选择最小均方误差(MSE)时的节点数作为最佳隐藏层节点。
1.3.3 SVM模型SVM的思想是寻找一个满足分类要求的最优分类超平面,使得该超平面在保证分类精度的同时,能够使超平面两侧的空白区域最大化。在构造最优决策函数时,利用了结构风险最小化原则[16]。影响模型性能的主要参数包括伽马(gamma)和代价(cost),前者控制分割超平面的形状,后者代表犯错的成本[17]。本研究改变参数组合尝试进行模型优化,预测性能未见显著提升,故模型建立中的gamma与cost均采用SVM函数的默认值,即gamma为预测变量个数的倒数(1/10)、cost默认值为1。
1.3.4 RF模型RF的基本思路是综合考虑多个决策树的结果,采用自助法(Bootstrap)即自采样的方法获得不同的样本集用于构建模型,从而确定最终RF算法的预测结果(图 1)。RF模型主要用于回归和分类,具有学习速度快和防止过拟合等特点。RF的2个重要参数为节点数(mtry)和决策树个数(ntree),mtry设为1~10,ntree为0~1 000,将MSE值最小时的mtry和ntree分别作为节点中用于二叉树的最佳变量个数和最佳决策树数目,5种金属元素Sb、As、Pb、Cd、Tl最佳mtry分别为2,4,6,6,3;最佳ntree分别为200,382,215,77,417。
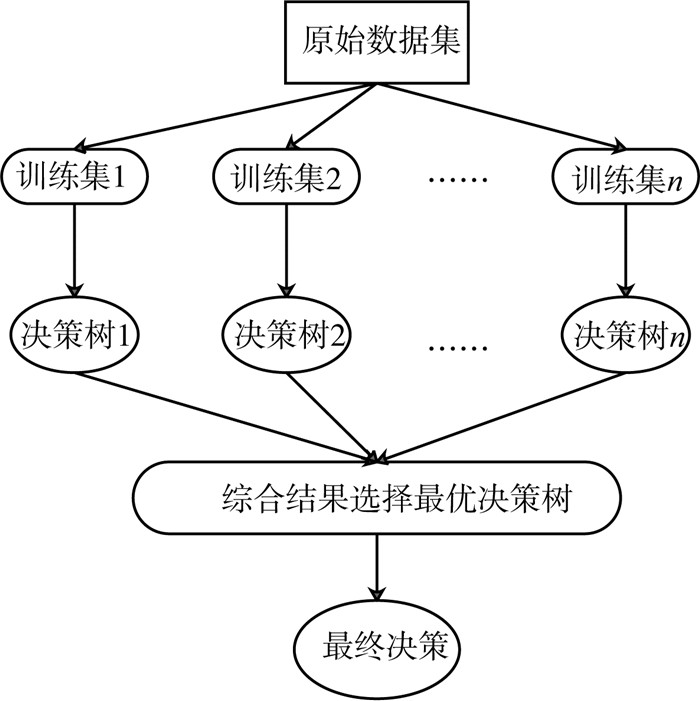
|
图 1 RF建模过程示意 |
模型评价指标包括相关系数(r)、平均绝对误差(MAE)和均方根误差(RMSE)[18]。r用于度量实际观测值和模型预测值之间的相似性,值越接近1,相似性越大。MAE和RMSE用于评价模型的预测有效性。MAE和RMSE可测量剩余误差(残差),二者都提供了观测数据和预测数据之间差异的全局估计。r值越接,近于1以及MAE和RMSE值越小代表模型预测效果越好。
2 结果与讨论 2.1 数据基本特征及相关性采样期间,ρ(PM2.5)为93.47 μg/m3,其中金属成分ρ(Sb)、ρ(As)、ρ(Cd)、ρ(Pb)、ρ(Tl)的日平均值分别为3.59,14.61,0.92,54.35,0.67 ng/m3。采样期间,ρ(PM2.5)月均值的时间序列见图 2,ρ(PM2.5)及其中金属质量浓度年均值的时间序列见图 3(a)(b)。由图 2、3可见,ρ(PM2.5)及其金属成分ρ(Sb)、ρ(As)、ρ(Cd)、ρ(Pb)、ρ(Tl)总体呈下降趋势。
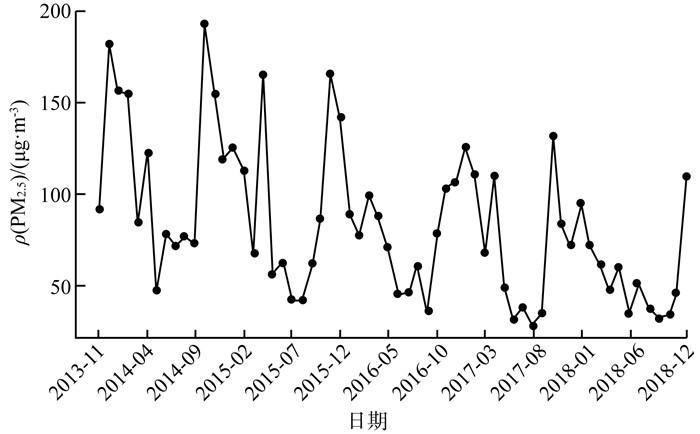
|
图 2 ρ(PM2.5)月均值的时间序列 |
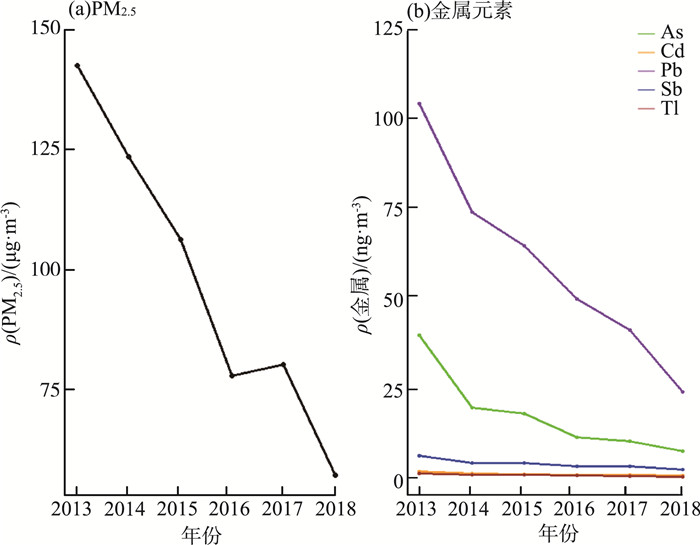
|
图 3 ρ(PM2.5)及其中金属质量浓度年均值的时间序列 |
采样期间,4个季节ρ(PM2.5)及其中金属质量浓度的箱线图见图 4(a)—(f)。由图 4可见,PM2. 5及其金属的质量浓度具有相似的季节变化模式,均表现为冬季最高,夏季最低。
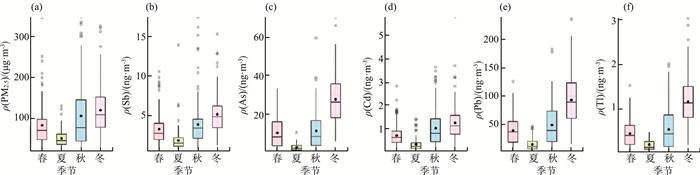
|
图 4 4个季节ρ(PM2.5)及其中金属质量浓度的箱线图 |
采样期间,PM2.5及其金属、气象因素及大气污染物的基本情况见表 1。由表 1可见,ρ(NO2)、ρ(SO2)、ρ(CO)、ρ(PM10)的日平均值分别为52.59 μg/m3,46.21 μg/m3,1.20 mg/m3,99.30 μg/m3。日平均温度、湿度、气压、风速、日照时间分别为1.24 ℃,66.57%,1 001.06 hPa,2.62 m/s和5.41 h。
| 表 1 PM2.5及其金属、气象因素及大气污染物的基本情况 |
PM2.5及其金属、大气污染物及气象因素之间Spearman秩相关分析结果见图 5。由图 5可见,PM2.5中金属与5种大气污染物之间正相关,相关系数为0.48~0.89,均有统计学意义。金属与温度负相关(-0.55~-0.79),与气压正相关(0.52~0.65),金属与其他气象因素的相关性较小。
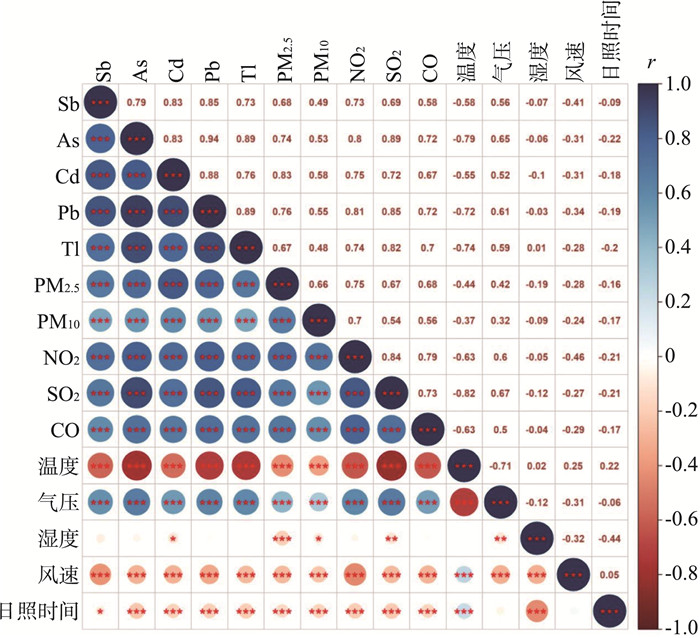
|
图 5 PM2.5及其金属、气象因素及大气污染物之间的相关性
注:圆圈大小代表相关系数的大小,圆圈里的* * *表示 P<0.001,* *表示P<0.01,*表示P<0.05。 |
由于数据收集的局限性,仅Sb、As、Cd、Pb、Tl 5种金属与输入变量相关性较大,最终仅选择这5种金属作为预测变量,对这5种金属进行4种方法模型的评价指标比较,以选择出最优方法(表 2)。由表 2可见,RF模型在5种金属的训练集和测试集中表现均比较稳定,其中r值均>0.7,同时MAE和RMSE相较于其他模型而言数值更小,由此可见RF模型预测效果最好。此外,3种机器学习方法(BP-ANN、SVM和RF)均优于传统方法(MLR)。
| 表 2 4种方法模型评价指标比较 |
MLR模型评价指标结果显示,r值在训练集为0.68~0.90,在测试集为0.72~0.92;MAE值在训练集为0.47~54.02,在测试集为0.48~55.46;RMSE值在训练集为0.57~65.93,在测试集为0.37~69.70(表 2)。以实际观测浓度值为横坐标,预测浓度值为纵坐标,MLR模型训练集和测试集中重金属浓度的观测值和预测值拟合情况见图 6(a)—(e)。
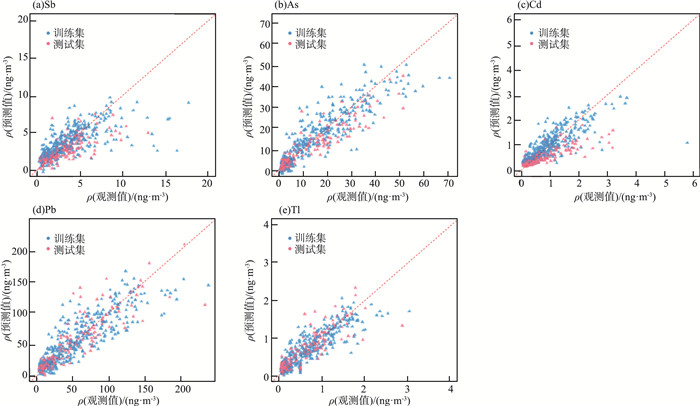
|
图 6 MLR模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况 |
由图 6可见,MLR模型评价指标中MAE和RMSE值较大,对PM2.5中金属质量浓度的预测值不是很理想。因此,有必要建立非线性模型来更好地拟合数据。研究结果显示,相比于MLR而言,RF、BP-ANN和SVM表现出较好的预测效果,MAE和RMSE显著降低。Leng等[11]使用MLR、BP-ANN和SVM 3种模型对南京市PM2.5中金属浓度的预测效果进行比较,同样发现MLR对于PM2.5中金属浓度的预测效果不佳。MLR作为经典的统计学方法,对于存在线性关系时仍然是一个可靠的预测模型,其可以计算出各个变量在模型中的系数大小,对模型解释性也较强。但MLR对于非线性问题时表现往往不佳[19]。因此,研究发现环境污染物预测较为复杂,传统的MLR几乎不适用,须通过可处理复杂的非线性动力系统的机器学习方法加以弥补。
2.2.3 BP-ANN模型评价BP-ANN模型中Sb、As、Cd、Pb、Tl最佳隐藏层节点数分别为12,14,14,14,14。模型评价指标结果显示r值在训练集为0.90~0.97,在测试集为0.71~0.85;MAE值在训练集为0.14~8.16,在测试集为0.43~23.34;RMSE值在训练集为0.19~11.17,在测试集为0.53~40.02(表 2)。BP-ANN模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况见图 7(a)—(e)。
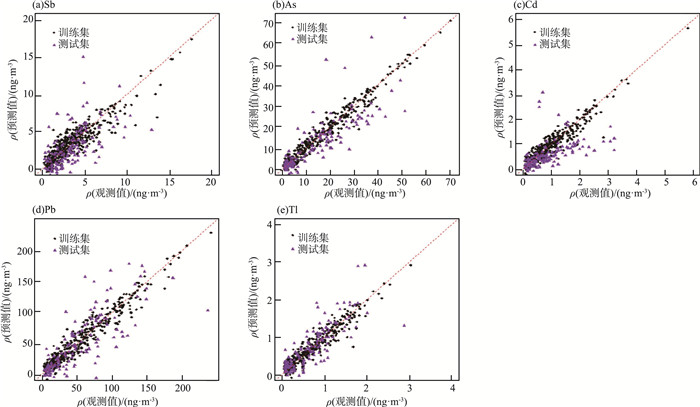
|
图 7 BP-ANN模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况 |
由图 7可见,BP-ANN模型在测试集的表现明显差于训练集的表现,这也是BP-ANN模型的主要缺点,模拟预测过程容易出现过拟合问题[20]。机器学习领域,BP-ANN在网络理论和性能方面已比较成熟,数学理论已证明它具有实现任何复杂非线性映射的功能,因此它适合于求解内部机制复杂的问题[20]。但BP-ANN也存在明显的缺陷,BP神经网络对初始网络权重非常敏感,以不同的权重初始化网络,容易出现过拟合和陷入局部极小值[21],因此本研究中BP-ANN出现的过拟合问题是由算法本身的特点所决定的。此外,BP-ANN学习速度慢,即使是一个简单的问题,一般也需要几百次甚至上千次的学习才能收敛。这主要是由于BP神经网络算法本质上为梯度下降法,它所要优化的目标函数非常复杂,所以收敛速度很慢[22]。
2.2.4 SVM模型评价SVM模型评价指标结果显示,r值在训练集为0.77~0.95,在测试集为0.72~0.91;MAE值在训练集为0.21~17.09,在测试集为0.30~25.97;RMSE值在训练集为0.13~10.67,在测试集为0.20~16.51(表 2)。SVM模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况见图 8(a)—(e)。
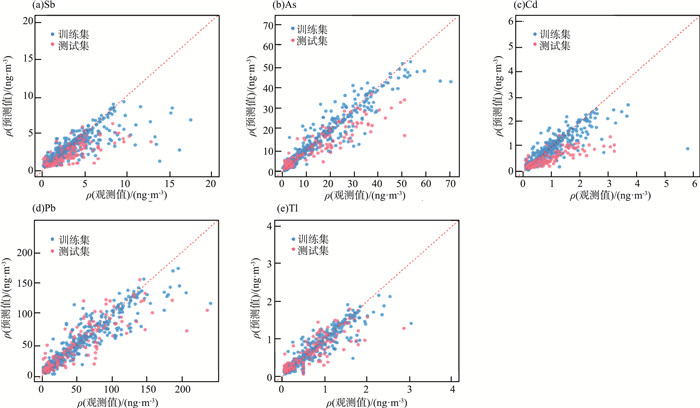
|
图 8 SVM模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况 |
由图 8可见,SVM模型在测试集的表现稍差于训练集,但与BP-ANN相比较而言,过拟合现象并不明显。该算法可最终转化为凸优化问题,因而可保证算法的全局最优性,避免了BP-ANN无法解决的局部最小问题[12]。Leng等[11]研究显示SVM较BP-ANN效果更好,成功应用SVM模型进行PM2.5中金属浓度的预测,避免了局部极小值问题。值得注意的是,该研究收集的PM2.5样本为328份,样本量相对较小时可利用SVM进行准确预测。但SVM算法对大规模训练样本难以实施,当观测样本较大时,SVM效率并不高,且SVM对于核函数的高维映射解释力不强[23]。
SVM模型中的重要参数为cost与gamma[24]。其中,cost是惩罚系数,即对误差的宽容度。cost越大,说明越不能容忍出现误差,容易过拟合,而cost越小,越容易欠拟合,cost过大或过小可能导致泛化能力变差[24]。gamma是选择径向基函数(RBF)作为核函数(kernel)后,该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布,gamma越大,支持向量越少,gamma值越小,支持向量越多,支持向量的个数影响训练与预测的速度[25]。参数选择对于最终预测结果有一定影响,本研究改变参数组合,尝试进行模型优化的过程中预测性能未见显著提升,所以2个参数大小都设置为默认值,这可能是预测效果降低的原因[26]。因此建议未来研究可通过尝试不同的输入变量组合和参数从而选择最佳预测模型,提高模型的预测能力。
2.2.5 RF模型评价5种金属(Sb、As、Cd、Pb、Tl)最佳mtry分别为2,4,6,6,3;最佳ntree分别为200,382,215,77和417。RF模型评价指标结果显示,r值在训练集为0.96~0.99,在测试集为0.71~0.91;MAE值在训练集为0.12~9.47,在测试集为0.29~23.88;RMSE值在训练集为0.08~6.50,在测试集为0.20~15.03(表 2)。RF在训练集表现极好,全部金属的r值均>0.9,RF模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况见图 9(a)—(e)。
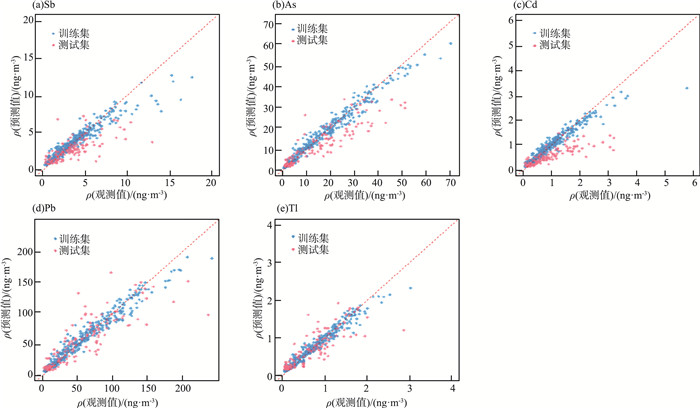
|
图 9 RF模型训练集和测试集中金属质量浓度的观测值和预测值拟合情况 |
由图 9可见,RF较SVM和BP-ANN在对PM2.5中金属质量浓度进行预测时效果更好。RF作为目前极为强大的机器学习方法之一,其在以决策树为基分类器进行集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。相较于BP-ANN和SVM模型而言具有不用降维即可处理高维度(特征很多)数据的特点,不易过拟合,同时训练速度比较快,以弥补BP-ANN和SVM效率不高的问题[27]。此外,对于不平衡的数据集来说,它可以平衡误差,从而提高预测的准确度[28]。上述优势可能是本研究中RF较SVM和BP-ANN表现更好的原因。陈金车等[29]对西北省会城市SO2、NO2、O3、CO、PM10和PM2.5 6种污染物的日均浓度值进行预测,对比RF和SVM模型,发现RF预测效果优于SVM。目前缺少RF应用于PM2.5中金属浓度的其他类似研究,因此建议未来可增加多种模型进行PM2.5中金属浓度的预测研究,从而筛选出最佳模型。
2.3 研究局限本研究尚存在以下不足。首先,PM2.5中金属浓度受政策、经济水平、人口、气象条件及土地利用等多种因素影响,由于收集数据的局限性,本研究仅纳入空气污染物和气象因素作为输入变量,且数据仅来源于单一城市,结果受样本量以及无外部验证数据集的影响,因此建议未来可增加多个城市的研究,将潜在影响因素纳入模型及增加样本量,在更高维度上拟合数据,为PM2.5中金属浓度的分析、评估及预测提供更多的思路。其次,虽然本研究使用了目前推荐的误差最小原则选择参数并进行了不同尝试,但仍未能涵盖所有可实现的预测模型,建议未来可通过尝试不同的输入变量组合和参数从而选择最佳预测模型,提高模型的预测能力。
3 结论(1) 2013—2018年哈尔滨市PM2.5及其金属浓度[ρ(Sb)、ρ(As)、ρ(Cd)、ρ(Pb)、ρ(Tl)]总体呈下降趋势。PM2.5和其金属质量浓度具有相似的季节模式,均表现为冬季最高,夏季最低。
(2) 采用4种预测模型(BP-ANN、SVM、RF和MLR)对哈尔滨市2013—2018年PM2.5中5种金属浓度的预测效果进行比较,发现传统MLR相较于机器学习方法整体预测性能差。因此,针对环境污染物的预测而言,传统的MLR几乎不适用,需要可处理复杂的非线性动力系统的机器学习方法加以弥补。
(3) 通过4种预测模型比较,发现RF模型总体预测效果最好,该模型在训练集和测试集中的表现均较好。RF模型拥有较好的泛化性、稳健性,能够在原理层面规避异常数据造成的模型过拟合或欠拟合而影响模型性能。本研究可在缺乏监测和实验数据的情况下,实现对大气颗粒物中金属浓度的快速预测,为更全面了解颗粒物中金属污染特征提供数据基础。但本研究数据仅来源于单一城市,受样本量以及无外部验证数据集的影响,结果具有一定局限性,需要进一步研究进行证实。
| [1] |
HAYES R B, LIM C, ZHANG Y, et al. PM2.5 air pollution and cause-specific cardiovascular disease mortality[J]. International Journal of Epidemiology, 2020, 49(1): 25-35. DOI:10.1093/ije/dyz114 |
| [2] |
BABATOLA S S. Global burden of diseases attributable to air pollution[J]. Journal of Public Health in Africa, 2018, 9(3): 813. |
| [3] |
BERGEN S, SHEPPARD L, SAMPSON P D, et al. A national prediction model for PM2.5 component exposures and measurement error-corrected health effect inference[J]. Environmental Health Perspectives, 2013, 121(9): 1017-1025. DOI:10.1289/ehp.1206010 |
| [4] |
TSENG C H. The potential biological mechanisms of arsenic-induced diabetes mellitus[J]. Toxicology and Applied Pharmacology, 2004, 197(2): 67-83. DOI:10.1016/j.taap.2004.02.009 |
| [5] |
HAN Q, LIU Y, FENG X, et al. Pollution effect assessment of industrial activities on potentially toxic metal distribution in windowsill dust and surface soil in central China[J]. Science of The Total Environment, 2021, 759: 144023. DOI:10.1016/j.scitotenv.2020.144023 |
| [6] |
DELAVAR M R, GHOLAMI A, SHIRAN G R, et al. A novel method for improving air pollution prediction based on machine learning approaches: A case study applied to the capital city of Tehran[J]. ISPRS International Journal of Geo-Information, 2019, 8(2): 99. DOI:10.3390/ijgi8020099 |
| [7] |
LI R, CUI L, LIANG J, et al. Estimating historical SO2 level across the whole China during 1973—2014 using random forest model[J]. Chemosphere, 2020, 247: 125839. DOI:10.1016/j.chemosphere.2020.125839 |
| [8] |
SHAMS S R, JAHANI A, KALANTARY S, et al. Artificial intelligence accuracy assessment in NO2 concentration forecasting of metropolises air[J]. Scientific Reports, 2021, 11(1): 1-9. DOI:10.1038/s41598-020-79139-8 |
| [9] |
YEGANEH B, MOTLAGH M S P, RASHIDI Y, et al. Prediction of CO concentrations based on a hybrid Partial Least Square and Support Vector Machine model[J]. Atmospheric Environment, 2012, 55: 357-365. DOI:10.1016/j.atmosenv.2012.02.092 |
| [10] |
LI H, WANG J, WANG Q, et al. Magnetic properties as a proxy for predicting fine-particle-bound heavy metals in a support vector machine approach[J]. Environmental Science & Technology, 2017, 51(12): 6927-6935. |
| [11] |
LENG X, WANG J, JI H, et al. Prediction of size-fractionated airborne particle-bound metals using MLR, BP-ANN and SVM analyses[J]. Chemosphere, 2017, 180: 513-522. DOI:10.1016/j.chemosphere.2017.04.015 |
| [12] |
QIAN X, YANG M, WANG C, et al. Leaf magnetic proper-ties as a method for predicting heavy metal concentrations in PM2.5 using support vector machine: A case study in Nanjing, China[J]. Environmental Pollution, 2018, 242: 922-930. DOI:10.1016/j.envpol.2018.07.007 |
| [13] |
杨华, 吴宇峰, 王静, 等. 超声提取-改进BCR法测定PM2.5中6种重金属元素的化学形态[J]. 理化检验: 化学分册, 2015, 51(8): 1154-1158. |
| [14] |
EBERLY L E. Multiple linear regression[J]. Topics in Biostatistics, 2007, 165-187. |
| [15] |
JAIN A K, MAO J, MOHIUDDIN K M. Artificial neural networks: A tutorial[J]. Computer, 1996, 29(3): 31-44. DOI:10.1109/2.485891 |
| [16] |
WIDODO A, YANG B S. Support vector machine in machine condition monitoring and fault diagnosis[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2560-2574. DOI:10.1016/j.ymssp.2006.12.007 |
| [17] |
ZHOU J, QIU Y, ZHU S, et al. Optimization of support vector machine through the use of metaheuristic algorithms in forecasting TBM advance rate[J]. Engineering Applications of Artificial Intelligence, 2021, 97: 104015. DOI:10.1016/j.engappai.2020.104015 |
| [18] |
KOUADRI S, ELBELTAGI A, ISLAM A R M, et al. Performance of machine learning methods in predicting water quality index based on irregular data set: application on Illizi region(Algerian southeast)[J]. Applied Water Science, 2021, 11(12): 1-20. |
| [19] |
AIKEN L S, WEST S G, PITTS S C. Multiple linear regression[J]. Handbook of Psychology, 2003(52): 481-507. |
| [20] |
LI Y, LI C, TAO J, et al. Study on spatial distribution of soil heavy metals in Huizhou city based on BP-ANN modeling and GIS[J]. Procedia Environmental Sciences, 2011, 10: 1953-1960. DOI:10.1016/j.proenv.2011.09.306 |
| [21] |
RODRIGUEZ-GALIANO V, SANCHEZ-CASTILLO M, CHICA-OLMO M, et al. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines[J]. Ore Geology Reviews, 2015, 71: 804-818. DOI:10.1016/j.oregeorev.2015.01.001 |
| [22] |
TANG T, LIU K, LI C, et al. Multi-channel optical sensing system with a BP-ANN for heavy metal detection[J]. Optics Express, 2022, 30(6): 9413-9427. DOI:10.1364/OE.451817 |
| [23] |
NOBLE W S. What is a support vector machine?[J]. Nature Biotechnology, 2006, 24(12): 1565-1567. DOI:10.1038/nbt1206-1565 |
| [24] |
KARATZOGLOU A, MEYER D, HORNIK K. Support vector machines in R[J]. Journal of Statistical Software, 2006, 15: 1-28. |
| [25] |
PISNER D A, SCHNYER D M. Machine Learning[M]. Academic Press, 2020: 101-121.
|
| [26] |
BENNETT-LENANE H, GRIFFIN B T, O'SHEA J P. Machine learning methods for prediction of food effects on bioavailability: A comparison of support vector machines and artificial neural networks[J]. European Journal of Pharmaceutical Sciences, 2022, 168: 106018. DOI:10.1016/j.ejps.2021.106018 |
| [27] |
BIAU G, SCORNET E. A random forest guided tour[J]. Test, 2016, 25(2): 197-227. DOI:10.1007/s11749-016-0481-7 |
| [28] |
COULSTON J W, BLINN C E, THOMAS V A, et al. Approximating prediction uncertainty for random forest regression models[J]. Photogrammetric Engineering & Remote Sensing, 2016, 82(3): 189-197. |
| [29] |
陈金车. 基于机器学习的西北省会城市空气污染物浓度预报方法研究[D]. 兰州: 兰州大学, 2022.
|
 2023, Vol. 15
2023, Vol. 15 

