大气二氧化碳(CO2)是主要的温室气体之一,近200年来,全球大气CO2柱浓度由280 ×10-6上升至约400×10-6[1],并且仍以每年约2×10-6的速率持续增加[2]。大气CO2浓度的增加加剧了全球温室效应,引起海平面上升、极端天气事件等一系列灾害[3]。因此,准确掌握大气CO2浓度及其变化情况,对于预测气候变化趋势、制定环境决策以及探索地球可持续发展具有重要意义。
卫星遥感技术可以提供长期连续且具有较高空间分辨率的全球观测,是深入了解大气CO2时空分布特征的重要手段之一,为碳监测研究、全球碳循环、气候变化和温室气体减排提供重要的科学观测数据[4-5]。近年来,国内外已发射了多个CO2探测卫星,并广泛地应用于全球气候变化研究,例如,日本于2009和2018年分别发射的温室气体观测卫星(GOSAT和GOSAT-2)[6],美国于2014年发射的轨道碳观测卫星-2(OCO-2)[7]以及于2019年搭载在国际空间站(ISS)的OCO-3 [8],中国于2017年发射的全球CO2监测科学实验卫星(TanSat)[9]等。上述卫星大多利用CO2在近红外波段的吸收效应,通过全物理模型,反演大气CO2平均干空气混合比(XCO2)。但是由于探测能力限制,仍存在覆盖范围和分辨率难以平衡的问题[4]。一些监测卫星通过离散采样点加大采样点之间距离以增加覆盖率(例如GOSAT、GOSAT-2),但使得空间分辨率较低(约10 km);另一些则采用窄幅(10~25 km)连续像素观测[如OCO-2、碳卫星搭载的大气二氧化碳光栅光谱仪(TanSat /ACGS)],但是轨道之间存在较多观测空白。研究表明,上述卫星XCO2产品中每日有效观测数据覆盖率不足1% [10],这对于研究全球高精度CO2时空分布是极大的挑战。
对此,研究者们提出了各种方法来重构高空间覆盖度的XCO2数据库[11]。例如,Guo等[12]通过建立XCO2与地表温度、植被指数、初级生产力等数据的线性关系,对全球CO2浓度进行评估;张丽丽等[13]使用高精度曲面建模来模拟XCO2的空间分布;Matloob等[14]使用地理加权回归的方法建立地表温度和XCO2的数值关系来分析工业区的碳排放;Jin等[10]使用最大似然估计(Maximum Likelihood Estimation)和最优插值(Optimal Interpolation)的方法对多源卫星XCO2产品进行集合处理,得到一个长期的、全球尺度的XCO2数据库。近年来,机器学习算法在XCO2模拟中也有越来越多的应用。相较于上述统计学方法,机器学习算法可以有效地处理复杂的非线性问题。例如,Zeng等[15]使用人工神经网络对海洋碳排放进行模拟;Siabi等[16]使用多层感知器对OCO-2 XCO2产品进行空间重构并进行分析;He等[17]使用Light GBM算法(Light Gradient Boosting Machine)对中国地区OCO-2 XCO2数据进行重构;Wang等[18]使用随机森林回归算法对京津冀地区XCO2数据进行插补。
针对目前OCO-2监测卫星数据的低空间覆盖度的问题,现基于多源卫星和模式数据,通过时间序列拟合以及随机森林回归算法,对中国地区2019—2022年碳监测卫星数据产品进行重构,并分析中国地区近年来XCO2的时空分布特征和未来发展趋势。研究成果可为碳监测研究、碳排放清单验证、碳排放管理、碳源碳汇动态分布、温室气体减排、辐射强迫和气候变化等相关研究提供重要的数据支撑。
1 数据与方法 1.1 数据来源与预处理本研究使用的数据包含OCO-2卫星快拍模式的XCO2,对流层监测仪(TROPOMI)反演到的二氧化氮对流层柱浓度(NO2 column density)和一氧化碳柱浓度(CO column density),美国CO2同化模拟系统(Carbon Tracker,CT)生成的XCO2数据和欧洲中期天气预报中心第5代(ERA-5)气象再分析资料。所有数据均覆盖2019年1月1日—2022年12月31日中国地区,具体数据和预处理方式如下。
1.1.1 OCO-2卫星XCO2数据XCO2数据来自OCO-2的OCO2_L2_Lite_FP.11r数据集。OCO-2是美国国家航空航天局(NASA)开发的太阳同步卫星,其搭载的三通道成像光栅式高光谱CO2探测仪空间分辨率为1.29 km×2.25 km,扫描幅宽为10.6 km[19-20]。为确保数据质量,仅使用质控标准(quality_flag)=0的数据产品进行分析。
1.1.2 欧洲哨兵5P卫星(Sentinel-5P)搭载的TROPOMI大气产品数据研究表明,在过去20年中,由化石燃料燃烧和工业过程产生的人为排放CO2占据了大气CO2总量的80%[21],而氮氧化物(NOx)和一氧化碳(CO)与人为排放CO2具有较强的同源性[22-25],因此,理论上通过NO2、CO和CO2的同步监测,可以有效地计算人为碳排放[26]。本研究选取TROPOMI的NO2和CO柱浓度L2离线数据产品[27-28]来表征人为碳排放的时空分布。TROPOMI搭载于极轨卫星Sentinel-5P上,其成像幅宽达2 600 km,可每日覆盖全球各地,原始数据最高空间分辨率为5.5 km×3.5 km[29]。为确保数据质量,仅选取质控标准(qa_value)≥0.5的数据产品进行分析。
1.1.3 CT XCO2数据相较于NO2等大气污染物,CO2具有显著的线性趋势、季节性以及较高的背景浓度[18, 30],而NO2、CO与CO2本地排放源的相关性更高[25]。因此,通常将XCO2拆分为背景值和距平值(XCO2与背景值的差值),以识别CO2的本地排放[30-32],XCO2的背景值有多种定义方式,本研究选用Hakkarainen等[30]的定义,即研究区域中XCO2的日中位数。由于OCO-2每日数据的覆盖度低,无法准确表征CO2的背景值,因此,使用CT的XCO2产品计算XCO2的背景值。CT同化了不同观测手段得到的XCO2数据,并广泛应用于CO2时空特征分析和监测数据对比验证工作。本研究使用CT2022 XCO2_1330LST产品,该产品可提供全球范围13:30时的XCO2,其空间分辨率为3°×2°[33]。目前CT数据只提供到2021年2月,考虑到XCO2具有显著的季节变化特征[34],因此,使用下式计算缺失时段的CT XCO2:
| $\begin{aligned} y & =a_1 \times \sin 2 \pi t+a_2 \times \cos 2 \pi t+a_3 \times \\ \sin 2 \pi t & +a_4 \times \cos 2 \pi t+a_5 \times t+a_6 \end{aligned} $ | (1) |
式中:y——CT拟合的XCO2,10-6;a1— a4——XCO2随季节变化的系数;a5——XCO2年内的线性增量,10-6/d;a6——XCO2的背景值,10-6;t——时间,d。为了证明NO2与CO对于预测CO2本地排放的作用,使用上述公式拟合的CT XCO2将与随机森林回归结果进行比较。
1.1.4 ERA-5气象再分析数据气象条件也是影响大气CO2浓度时空分布的重要因素之一。其中风速、温度和大气稳定度对于大气化学成分的浓度影响尤为重要[18, 35]。本研究使用ERA-5 Reanalysis气象再分析资料。ERA-5空间分辨率为0.25°×0.25°,时间分辨率最高可达1 h[36]。本研究选取ERA-5 Reanalysis近地面大气产品,包含2 m空气温度(t2m)、表面气压(sp)、边界层高度(blh)、10米u风分量和10米v风分量(u10,v10)。为确保再分析资料与卫星监测数据的一致性,选取每日东八区时间(UTC+8)13:00—14:00 (卫星过境时段)的平均值数据进行分析。
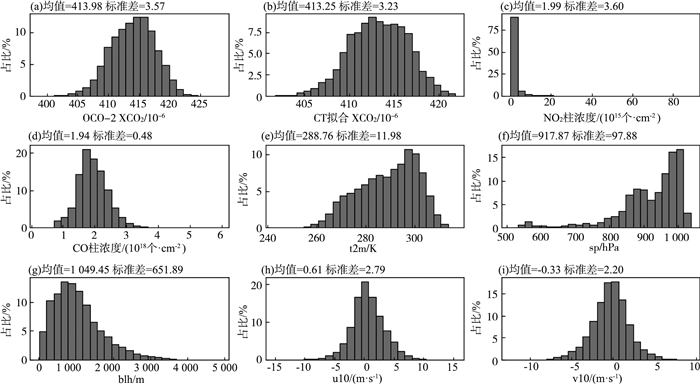
1.2 随机森林回归模型参数设置及评价指标选用随机森林(Random Forest,RF)回归模型[37-39]对XCO2进行空间重构。经过调研和分析[15-18, 40],选取TROPOMI NO2和CO柱浓度、CT2022 XCO2以及ERA-5气象参数(t2m、sp、blh、u10、v10)作为特征参数。将上述卫星和气象参数统一至0.05°×0.05°的日均数据集,最终得到95 108个样本。训练样本中各特征参数的统计见图 1(a)—(i)。
|
图 1 训练样本中各特征参数统计直方图 |
使用标准差法(Z-score normalization)对样本数据进行预处理:
| $ x^*=\frac{x-\mu}{\sigma} $ | (2) |
式中:x*——特征参数标准化后的结果;x——特征参数;μ、σ——特征参数的均值和标准差。
使用十折交叉验证(10-fold cross validation,10-CV)来选择超参数并检验RF回归模型,此方法可以有效防止算法过拟合问题。通过将样本分为10个子集,轮流使用9个子集训练模型,剩下的1个子集验证模型。10次结果的均值将作为对算法性能的评估,并从中选取最优模型。最终选取的RF模型参数分别为树的数量(n_estimators)=60,最大深度(max_depth)=40,叶子节点最少样本数(min_samples_leaf)=20。
模型的性能将由皮尔森(Pearson)决定系数(R2)、均方根误差(RMSE)和平均偏差(MB)来评估,计算公式如下:
| $ R^2=\left[\frac{\sum _{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum _{i=1}^n\left(x_i-\bar{x}\right)^2 \sum _{i=1}^n\left(y_i-\bar{y}\right)^2}}\right]^2 $ | (3) |
| $\text { RMSE }=\sqrt{\frac{\sum _{i=1}^n\left(y_i-x_i\right)^2}{n}} \\ $ | (4) |
| $ \begin{aligned} \operatorname{MB}=\frac{\sum _{i=1}^n\left(y_i-x_i\right)}{n} \end{aligned} $ | (5) |
式中:x,y——卫星反演和模型估算的XCO2,10-6;
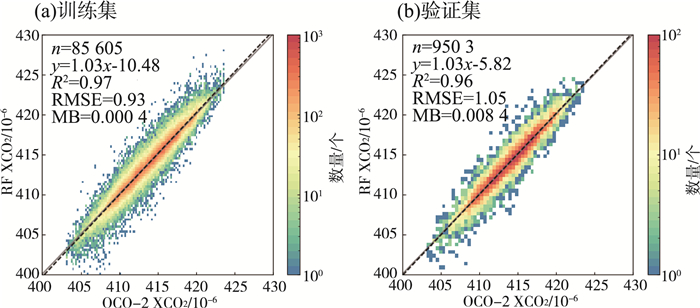
RF回归模型训练性能见图 2(a)(b)。由图 2(a)可见,在训练过程中,模型计算的XCO2(以下称为RF XCO2)与OCO-2反演的XCO2(以下称为OCO-2 XCO2)的R2高达0.97,RMSE为0.93×10-6,MB为0.000 4×10-6;由图 2(b)可见,在验证过程中,RF XCO2与OCO-2 XCO2的R2高达0.96,RMSE为1.05×10-6,MB为0.008 4×10-6,训练过程与验证过程的模型性能差异较小,过拟合问题的风险较低。同时,RF模型训练精度满足卫星遥感反演XCO2的精度要求(约1×10-6)[19-20],且本研究的模型精度优于Wang等[18]使用RF回归的结果(RMSE=1.68×10-6)。
|
图 2 RF回归模型性能 |
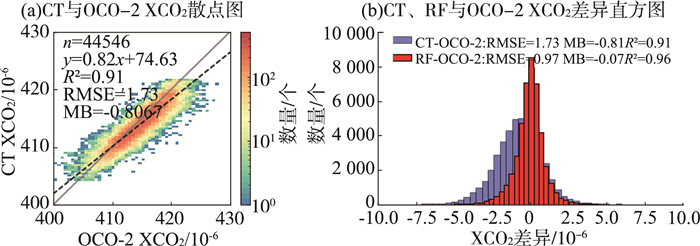
CT XCO2、RF XCO2与OCO-2 XCO2的结果比较见图 3(a)(b)。虽然CT XCO2与OCO-2 XCO2 XCO2的决定系数较高(R2=0.91),但是存在较大的系统偏差(RMSE=1.73×10-6),且整体偏低(MB=-0.81 ×10-6);相较而言,RF与OCO-2 XCO2的RMSE为0.97×10-6,MB为-0.07×10-6,R2高达0.96。由此可见,RF XCO2与卫星反演结果更加吻合。
|
图 3 CT XCO2、RF XCO2与OCO-2 XCO2结果比较 |
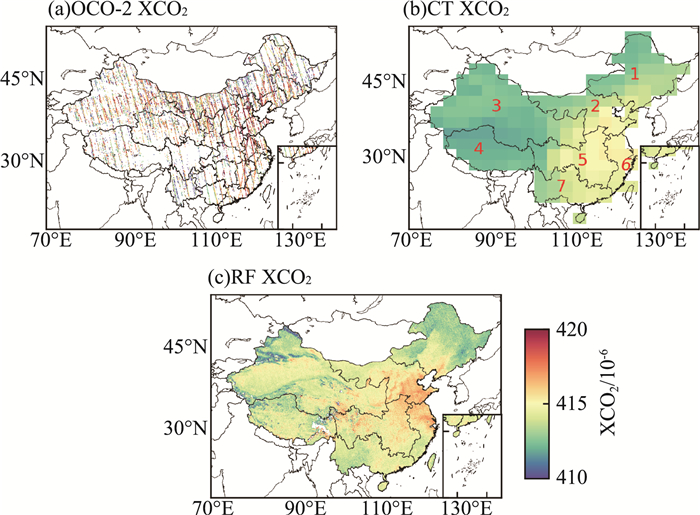
对比中国地区2019—2022年OCO-2、CT和RF XCO2多年平均空间分布情况可知[图 4(a)(b)(c)],由于OCO-2的幅宽较窄(10.6 km),重返周期长(16 d),其数据产品的空间覆盖度差,许多地区缺失有效的观测数据,无法呈现完整的XCO2空间分布特征;CT XCO2虽然能覆盖全国范围,但是空间分辨率低,难以描述中小尺度的空间分布;RF模型通过建立XCO2与其他具有高空间覆盖度、高空间分辨率的特征向量之间的数值关系,克服了XCO2数据覆盖度低、分辨率不足的问题,能够在较高的分辨率上反映全国XCO2的空间分布情况。
|
图 4 2019—2022年OCO-2、CT与RF XCO2多年平均空间分布图 注:1—东北;2—北部;3—西北;4—西南;5—中部;6—东部;7—南部;底图源自标准地图服务系统(http://bzdt.ch.mnr.gov.cn/),审图号为GS(2016)1549号,下同。 |
进一步将中国地区划分为东北、北部、西北、西南、中部、东部和南部区域[图 4(b)],并统计不同地区的CT、RF的XCO2差异,统计结果见表 1。由表 1可见,CT XCO2对于中国西部地区低估较为严重,其中西北和西南地区的MB均<-1.0 ×10-6,东北、东部地区的偏差相对较低,RMSE均<1.5 ×10-6;RF XCO2整体表现都优于CT XCO2,其中东北、北部、西北和东部地区的偏差相对较低,RMSE均<1.0×10-6。
| 表 1 2019—2022年中国各地区CT、RF与OCO-2 XCO2差异统计表 |
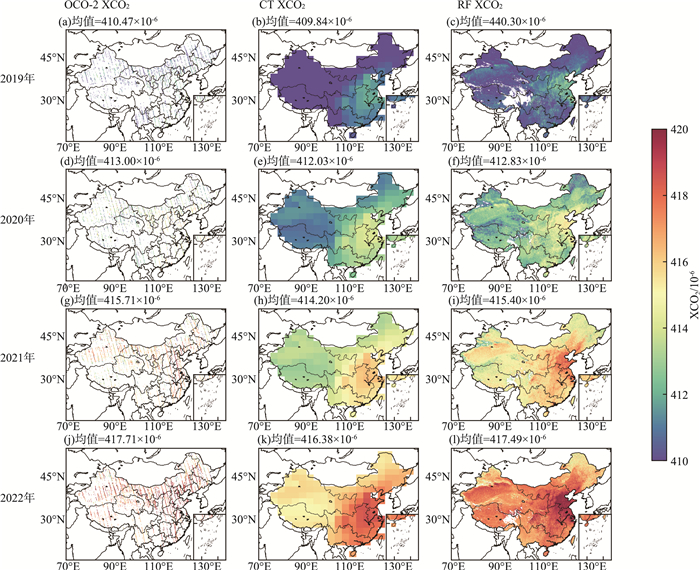
2019—2022年OCO-2、CT和RF XCO2空间分布情况见图 5(a)—(l)。由图 5可见,CT、RF XCO2均呈现逐年递增的趋势,与OCO-2反演结果一致。2019—2022年CT、RF与OCO-2 XCO2差异统计情况见表 2。由表 2可见,CT与OCO-2各年度的决定系数偏低(R2≤0.81),且相较于OCO-2,CT整体低估了中国地区的XCO2;2021年后,虽然CT与OCO-2 XCO2的相关系数有所增加,但RMSE和MB差异均高于2021年之前,表示近年来低估程度有增加的趋势;而RF XCO2表现则更为稳定,且与OCO-2 XCO2的一致性更好(R2均>0.90)。
|
图 5 2019—2022年OCO-2、CT和RF XCO2空间分布 |
| 表 2 2019—2022年CT、RF与OCO-2 XCO2差异统计 |
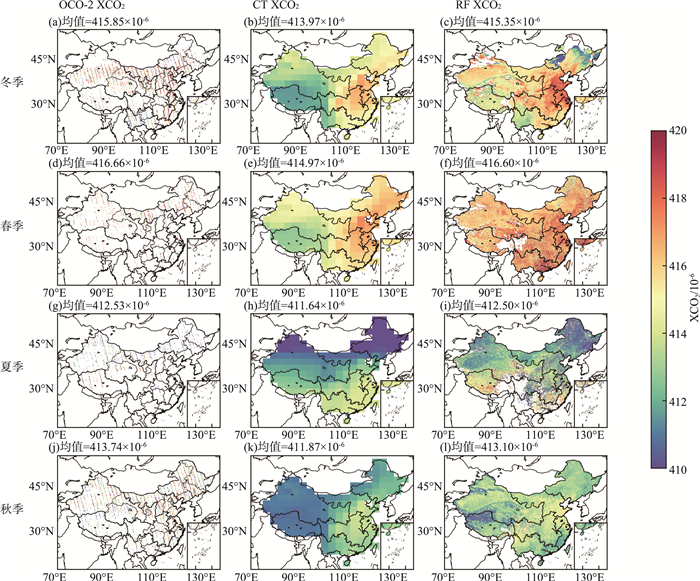
2019—2022年各季节OCO-2、CT和RF XCO2空间分布情况见图 6(a)—(l)。由图 6可见,冬、春季XCO2远高于夏、秋季。夏季,由于植被的光合作用活跃,使得大量CO2被植被吸收;相反,冬季低温抑制了植被的呼吸作用和光合作用,CO2在冬季累积并于春季达到峰值。CT与RF XCO2均体现了这个季节特征,且与其他研究成果中的结论相一致[11, 41-42]。
|
图 6 2019—2022年各季度OCO-2、CT与RF XCO2空间分布 注:冬季:1—2月、12月;春季:3—5月;夏季:6—8月;冬季:9—11月。 |
2019—2022年各季节CT、RF与OCO-2 XCO2差异统计情况见表 3。由表 3可见,CT与OCO-2 XCO2各季节的决定系数较高(R2均>0.88),但各季度均有不同程度的低估情况,低估区域主要出现在西北和西南地区。CT在春季表现较好,冬、秋季低估了中国西部、北部地区的XCO2,造成了MB<-0.85 ×10-6;而夏季则高估了中国东北和东部地区的XCO2,造成了夏季RMSE高达1.91 ×10-6。RF与OCO-2 XCO2整体相关性更好(R2均>0.95),除夏季外,RMSE均<1 ×10-6;夏季RMSE较高,可能由于夏季云量较大,观测数据较少,且夏季气溶胶对被动观测卫星的影响较大,降低了观测数据质量。整体而言,RF XCO2更接近OCO-2的季节分布特征,而CT XCO2在各个季节都低估了XCO2。
| 表 3 2019—2022年各季节CT、RF与OCO-2 XCO2差异统计 |
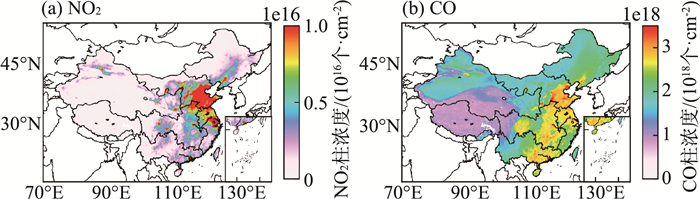
由图 5和图 6可知,CT XCO2在各年份的空间分布特征基本相似,整体而言中国沿海地区和中部地区的XCO2显著高于其他地区,东西差异显著;RF XCO2在各年份也呈现相似的空间分布特征,但东北、西北、西南地区也出现不同程度的XCO2高值,整体而言中国沿海地区和中部地区与其他地区的差异不如CT XCO2显著。从不同季节来看(图 6),CT XCO2在冬季、春季、秋季的分布情况相似,高值主要集中在中国东部、中部和北部沿海地区,夏季XCO2则呈现显著的由南向北递减的特征;RF XCO2除了上述特征外,冬季、春季和秋季的西北地区,春季和夏季的西南地区也出现XCO2高值,这些与OCO-2反演结果一致。中国东部、中部以及北部沿海地区一直为全国的高碳排地区[图 7(a)(b)],高度的人类活动是这些地区的XCO2高的主要原因[17];中国南方地区虽然有大量的生物质燃烧排放,但是由于植被覆盖率高,使得该地区XCO2处于中等水平[42];中国西部地区,由于化石燃料燃烧和生物质燃烧排放均较低,使得该地区的XCO2较低[17]。
|
图 7 2019—2022年TROPOMI NO2和CO柱浓度平均空间分布 |
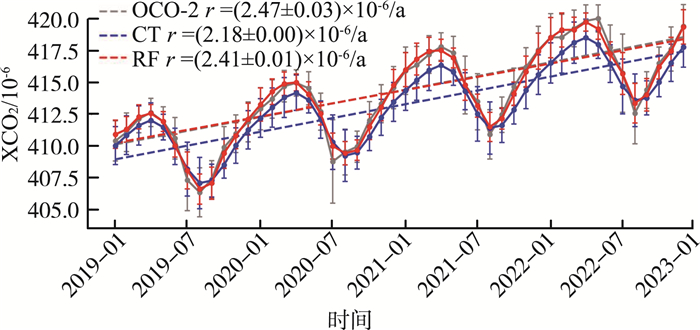
2019—2022年CT、RF与OCO-2 XCO2时间序列与趋势见图 8。由图 8可见,OCO-2、CT和RF XCO2的时间序列所展示的季节波动特征基本一致,但CT XCO2整体较低,其中冬、春季的差异最为显著。通过公式(1)的时间序列拟合,得到XCO2的线性增长速度(r)。从全国情况来看,中国地区RF XCO2以(2.41±0.01)×10-6/a的速度增长,其结果与OCO-2观测数据得到的线性增长速度接近[(2.47±0.03)×10-6/a],而CT的线性增长速度较慢,为(2.18±0.00)×10-6/a。尽管XCO2一直持续增加,但RF XCO2的增长率在降低,2019—2020年的增长率为(2.46±0.03)×10-6/a,而2021—2022年的增长率降至(2.09±0.03)×10-6/a,与OCO-2观测结果基本一致[2019—2020年和2021—2022年增长率分别为(2.50±0.10)×10-6/a和(2.17±0.1)×10-6/a],这可能与当年生产活动减少有关。
|
图 8 2019—2022年CT、RF与OCO-2 XCO2时间序列与趋势 |
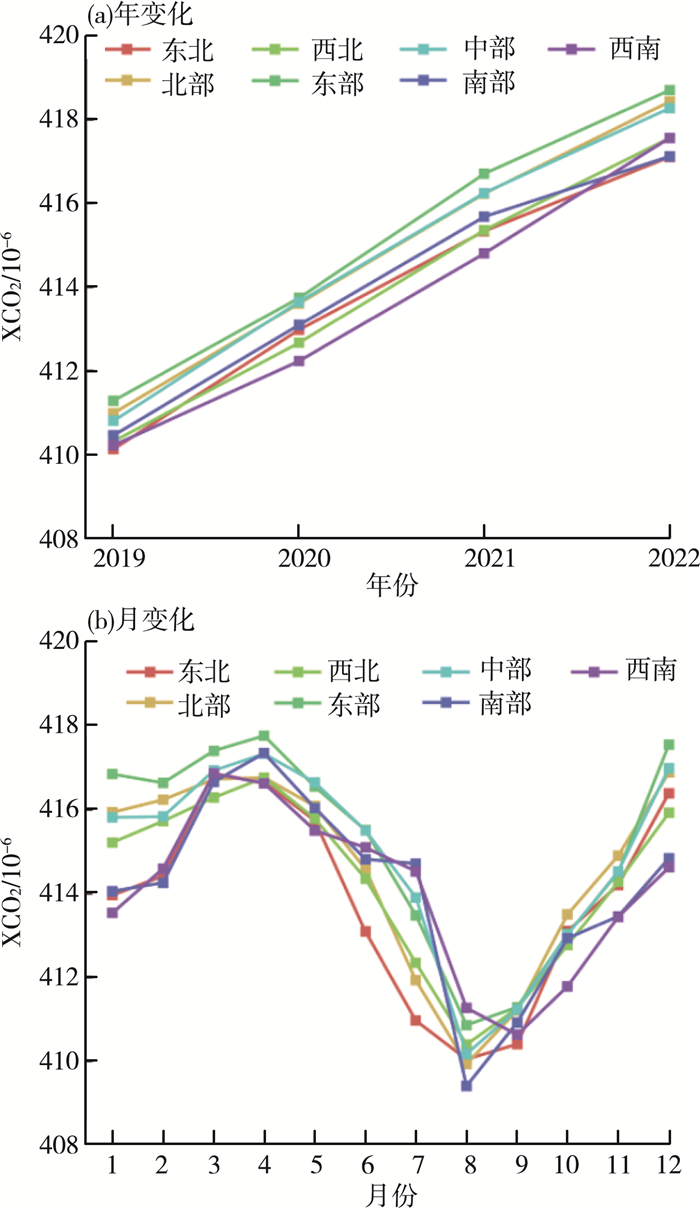
进一步基于RF XCO2分析2019—2022年中国各地区的年均增长曲线和月均变化曲线[图 9(a)(b)]。由图 9可见,2019—2022年,中国各地XCO2均呈现显著的上升趋势,每年月度变化特征基本一致。东部、北部、中部一直为中国XCO2高值地区;西北、东北和南部地区XCO2略低,且2021年后增长速率显著降低;西南地区XCO2为全国最低,但2021—2022年XCO2增长率有所增加。2019—2022年中国各地区OCO-2、CT与RF XCO2增长率见表 4。由表 4可见,中国东北、北部、东部和中部地区的RF XCO2增长率分别为(2.49±0.01)×10-6/a,(2.44±0.01)×10-6/a,(2.44±0.02) ×10-6/a和(2.42±0.02) ×10-6/a,高于西北[(2.39±0.01)×10-6/a]、南部[(2.36±0.02)×10-6/a]和西南[(2.33±0.01)×10-6/a]地区。OCO-2 XCO2显示增长率最高为中国北方(东北、北部和西北地区)以及中部地区,而CT XCO2在中国中部和东部的增长率最为显著。总体而言,RF XCO2增长率空间分布特征与OCO-2卫星反演结果一致性更高。
|
图 9 2019—2022年中国各地区RF XCO2年均和月均时间序列 |
| 表 4 2019—2022年各地区OCO-2、CT与RF XCO2增长率 |
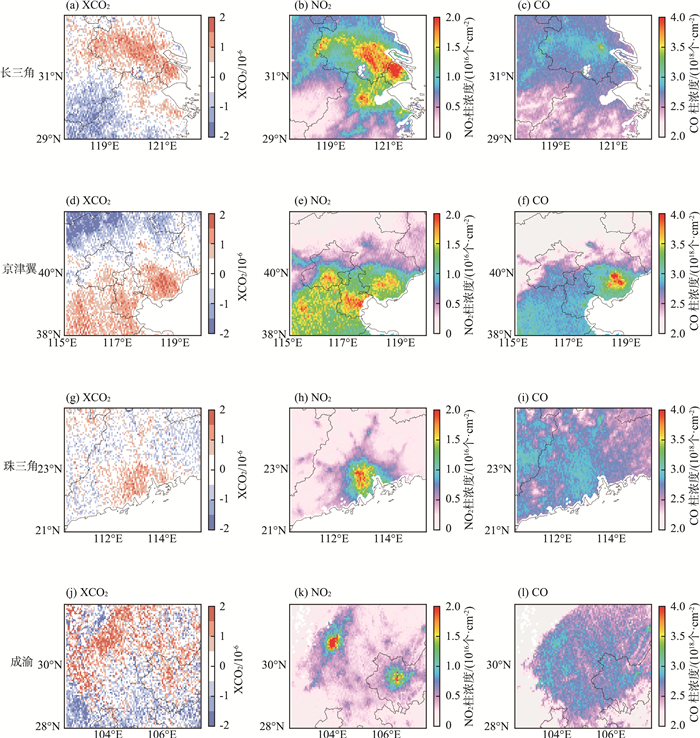
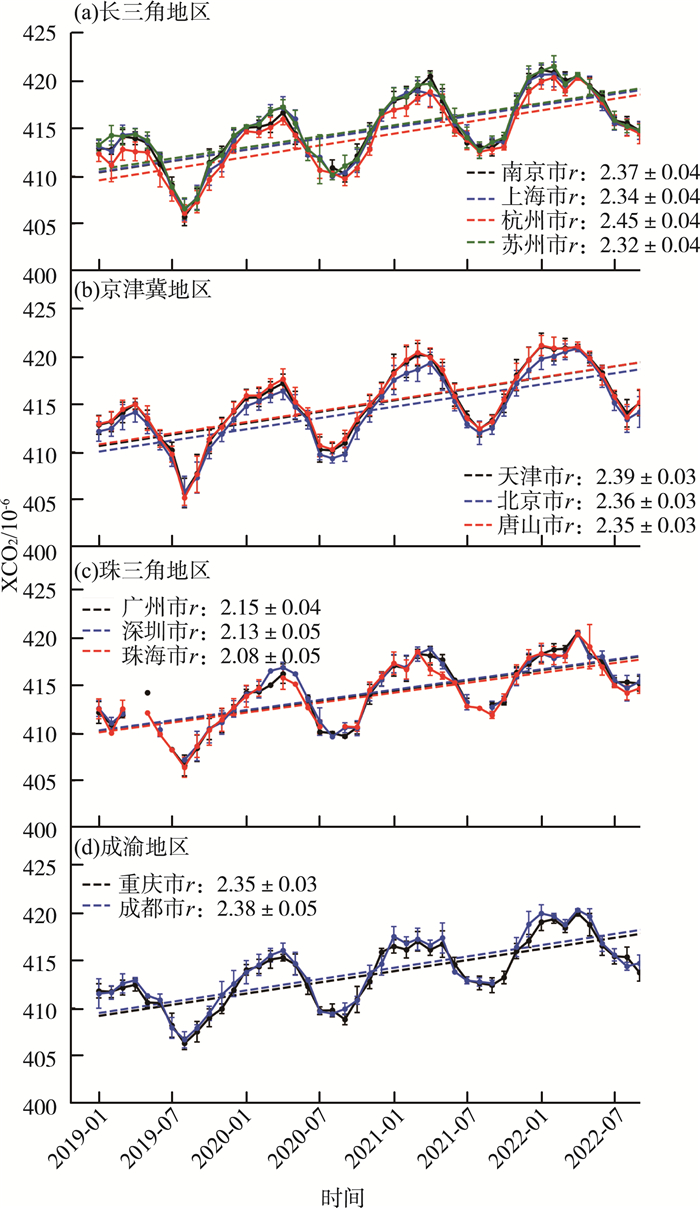
进一步选取中国四大经济圈,即长三角、珠三角、京津冀和成渝地区进行分析。这些地区人口密集,经济发达,城市化和工业化程度高,是重要的CO2人为源排放区域。2019—2022年我国典型地区XCO2距平分布见图 10(a)—(l)。为更好地显示CO2局地人为排放与NO2和CO柱浓度的关系,此处使用XCO2距平(去背景值)表征XCO2的空间分布。由图 10可见,RF XCO2距平与NO2、CO柱浓度具有较好的空间对应关系,可以一定程度反映人为排放的空间分布。以长三角地区为例,江苏沿江地区、上海以及浙江北部地区的NO2和/或CO柱浓度显著高于其他地区,使得这些地区XCO2较该区域均值高出约1.5×10-6。2019—2022年我国典型地区重构XCO2时间序列和增长趋势见图 11(a)—(d)。由图 11可见,总体而言,长三角和京津冀地区的XCO2绝对值水平高于珠三角和成渝地区;京津冀和成渝地区的增长率最高(均>2.35 ×10-6/a),其中天津和成都的增长率最高,接近2.40 ×10-6/a;长三角地区增长率在2.35×10-6/a左右,其中杭州市的XCO2虽然低于其他城市,但其增长率高达(2.45±0.04)×10-6/a,未来有赶超长三角其他城市的趋势;珠三角地区的增长率最低,约为2.10 ×10-6/a;京津冀地区的季节波动幅度较其他南方地区更为显著,这与其他研究中的结论一致[18];各地区的XCO2及其增长率特征符合先前的分析结果。
|
图 10 2019—2022年我国典型地区RF XCO2距平分布 |
|
图 11 2019—2022年我国典型地区重构XCO2时间序列和增长趋势 |
卫星遥感作为主要的温室气体观测手段之一,在大尺度全球观测方面拥有独特的优势。目前由于探测技术的限制,温室气体观测卫星存在空间覆盖范围和空间分辨率之间平衡的问题。本研究中使用的OCO-2观测卫星拥有较高的空间分辨率,但是其轨道之间存在大量的观测空白,数据的空间覆盖度低。面对此问题,结合多源卫星和模式数据优势,使用时间序列拟合和RF回归模型,重构了2019—2022年中国地区0.05°×0.05° XCO2的空间分布,并基于此分析近年来中国地区CO2时空变化特征。结论如下:
(1) RF XCO2可以在较高空间分辨率上体现中国地区XCO2的时空分布情况,且相较于CT,RF与OCO-2的观测结果一致性更高,其中东北、北部、东部和西北地区的偏差相对较低(RMSE均<1.0×10-6),而夏季由于云量和气溶胶对被动观测卫星的影响较大,导致偏差相对较大(RMSE=1.28×10-6)。
(2) 基于RF XCO2结果得知,中国地区XCO2呈现明显的季节性波动,XCO2冬春高、夏秋低;中国东部、北部、中部地区的XCO2显著高于其他地区,这些地区人为活动密集,为全国的高碳排地区。
(3) 2019—2022年,中国地区XCO2呈现逐年上升的趋势,增长速率达到(2.41±0.01)×10-6/a,但近年来增长速率有所降低;中国东部、北部、中部地区的XCO2增长率较高(>2.40×10-6/a);进一步分析中国典型经济区的XCO2,发现杭州、天津、成都的XCO2在各经济区内的增长最为迅速。
| [1] |
BALLANTYNE A P, ALDEN C B, MILLER J B, et al. Increase in observed net carbon dioxide uptake by land and oceans during the past 50 years[J]. Nature, 2012, 488(7409): 70-72. DOI:10.1038/nature11299 |
| [2] |
KAPPELLE M. WMO statement on the state of the global climate in 2019[J]. World Meteorological Organization, Geneva, Switzerland, 2020. |
| [3] |
DIETZ S, BOWEN, A, DIXON C, et al. Climate value at risk of global financial assets[J]. Nature Climate Change, 2016, 6(7): 676-679. DOI:10.1038/nclimate2972 |
| [4] |
刘毅, 王婧, 车轲, 等. 温室气体的卫星遥感——进展与趋势[J]. 遥感学报, 2021, 25(1): 53-64. |
| [5] |
杨晓钰, 王中挺, 潘光, 等. 卫星遥感温室气体的大气观测技术进展[J]. 大气与环境光学学报, 2022, 17(6): 581-597. |
| [6] |
NAKAJIMA M, SUTO H, YOTSUMOTO K, et al. Fourier transform spectrometer on GOSAT and GOSAT-2[C]//International Conference on Space Optics—ICSO 2014. SPIE, 2017, 10563: 1354-1362.
|
| [7] |
CRISP D, POLLOCK H R, ROSENBERG R, et al. The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products[J]. Atmospheric Measurement Techniques, 2017, 10(1): 59-81. DOI:10.5194/amt-10-59-2017 |
| [8] |
ELDERING A, TAYLOR T E, O'DELL C W, et al. The OCO-3 mission: measurement objectives and expected performance based on 1 year of simulated data[J]. Atmospheric Measurement Techniques, 2019, 12(4): 2341-2370. DOI:10.5194/amt-12-2341-2019 |
| [9] |
YANG D, LIU Y, CAI Z, et al. First global carbon dioxide maps produced from TanSat measurements[J]. Advances in Atmospheric Sciences, 2018, 35(6): 621-623. DOI:10.1007/s00376-018-7312-6 |
| [10] |
JIN C, XUE Y, JIANG X, et al. A long-term global XCO2 dataset: Ensemble of satellite products[J]. Atmospheric Research, 2022, 279: 106385. DOI:10.1016/j.atmosres.2022.106385 |
| [11] |
PEI Z, HAN G, MA X, et al. A method for estimating the background column concentration of CO2 using the lagrangian approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-12. |
| [12] |
GUO M, WANG X, LI J, et al. Assessment of global carbon dioxide concentration using MODIS and GOSAT data[J]. Sensors (Switzerland), 2012, 12(12): 16368-16389. DOI:10.3390/s121216368 |
| [13] |
张丽丽, 赵明伟, 赵娜, 等. 基于OCO-2卫星观测模拟高精度XCO2的空间分布[J]. 地球信息科学学报, 2018, 20(9): 1316-1326. |
| [14] |
MATLOOB A, SARIF M O, UM J S. Evaluating the inter-relationship between OCO-2 XCO2 and MODIS-LST in an industrial belt located at Western Bengaluru City of India[J]. Spatial Information Research, 2021, 29: 257-265. DOI:10.1007/s41324-021-00396-4 |
| [15] |
ZENG J, NOJIRI Y, NAKAOKA S, et al. Surface ocean CO2 in 1990—2011 modelled using a feed-forward neural network[J]. Geoscience Data Journal, 2015, 2(1): 47-51. DOI:10.1002/gdj3.26 |
| [16] |
SIABI Z, FALAHATKAR S, ALAVI S J. Spatial distribution of XCO2 using OCO-2 data in growing seasons[J]. Journal of Environmental Management, 2019, 244: 110-118. |
| [17] |
HE C, JI M, LI T, et al. Deriving full-coverage and fine-scale XCO2 across China based on OCO-2 satellite retrievals and carbon tracker output[J]. Geophysical Research Letters, 2022, 49(12): e2022GL098435. DOI:10.1029/2022GL098435 |
| [18] |
WANG W, HE J, FENG H, et al. High-coverage reconstruction of XCO2 using multisource satellite remote sensing data in Beijing-Tianjin-Hebei Region[J]. International Journal of Environmental Research and Public Health, 2022, 19(17): 10853. DOI:10.3390/ijerph191710853 |
| [19] |
CRISP D, BÖSCH H, BROWN L, et al. OCO-2 level 2 full physics retrieval algorithm theoretical basis[R]. Jet Propulsion Laboratory, NASA: Pasadena, CA, USA, 2010.
|
| [20] |
CRISP D. Measuring atmospheric carbon dioxide from space: The GOSAT and OCO-2 missions[C]//Optical instrumentation for energy and environmental applications. Optica Publishing Group, 2011: EWC6.
|
| [21] |
LE QUÉRÉ C, ANDREW R M, CANADELL J G, et al. Global carbon budget 2016[J]. Earth System Science Data, 2017, 15(8): 605-649. |
| [22] |
PALMER P I, SUNTHARALINGAM P, JONES D B A, et al. Using CO2: CO correlations to improve inverse analyses of carbon fluxes[J]. Journal of Geophysical Research: Atmospheres, 2006, 111(D12): 1-11. |
| [23] |
WUNCH D, WENNBERG P O, TOON G C, et al. Emissions of greenhouse gases from a North American megacity[J]. Geophysical Research Letters, 2009, 36(15): 1-5. |
| [24] |
HEDELIUS J K, LIU J, ODA T, et al. Southern California megacity CO2, CH4, and CO flux estimates using ground- and space-based remote sensing and a Lagrangian model[J]. Atmospheric Chemistry and Physics, 2018, 18(22): 16271-16291. DOI:10.5194/acp-18-16271-2018 |
| [25] |
WU D, LIU J, WENNBERG P O, et al. Towards sector-based attribution using intra-city variations in satellite-based emission ratios between CO2 and CO[J]. Atmospheric Chemistry and Physics, 2022, 22(22): 14547-14570. DOI:10.5194/acp-22-14547-2022 |
| [26] |
HONG Z, HU Y, CUI C, et al. An operational downscaling method of solar-induced chlorophyll fluorescence (SIF) for regional drought monitoring[J]. Agriculture, 2022, 12(4): 547. DOI:10.3390/agriculture12040547 |
| [27] |
VAN GEFFEN J, BOERSMA K F, ESKES H, et al. S5P TROPOMI NO2 slant column retrieval: Method, stability, uncertainties and comparisons with OMI[J]. Atmospheric Measurement Techniques, 2020, 13(3): 1315-1335. DOI:10.5194/amt-13-1315-2020 |
| [28] |
LANDGRAF J, DE BRUGH J A, SCHEEPMAKER R, et al. Algorithm theoretical baseline document for sentinel-5 precursor: Carbon monoxide total column retrieval[J]. Sorbonnelaan, 2018(2): 3584. |
| [29] |
VEEFKIND J P, ABEN I, MCMULLAN K, et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications[J]. Remote Sensing of Environment, 2012, 120: 70-83. DOI:10.1016/j.rse.2011.09.027 |
| [30] |
HAKKARAINEN J, IALONGO I, TAMMINEN J. Direct space-based observations of anthropogenic CO2 emission areas from OCO-2[J]. Geophysical Research Letters, 2016, 43(21): 11400-11406. |
| [31] |
HAKKARAINEN J, IALONGO I, MAKSYUTOV S, et al. Analysis of four years of global XCO2 anomalies as seen by orbiting carbon observatory-2[J]. Remote Sensing, 2019, 11(7): 850. DOI:10.3390/rs11070850 |
| [32] |
ZHENG B, CHEVALLIER F, CIAIS P, et al. Observing carbon dioxide emissions over China's cities and industrial areas with the Orbiting Carbon Observatory-2[J]. Atmospheric Chemistry and Physics, 2020, 20(14): 8501-8510. DOI:10.5194/acp-20-8501-2020 |
| [33] |
JACOBSON A R, SCHULDT K N, MILLER J B, et al. Carbon Tracker CT2019[R]. NOAA Earth System Research Laboratory, Global Monitoring Division: Boulder, CO, USA, 2020.
|
| [34] |
KEELING C D, BACASTOW R B, BAINBRIDGE A E, et al. Atmospheric carbon dioxide variations at Mauna Loa observatory, Hawaii[J]. Tellus, 1976, 28(6): 538-551. DOI:10.1111/j.2153-3490.1976.tb00701.x |
| [35] |
SIABI Z, FALAHATKAR S, ALAVI S J. Spatial distribution of XCO2 using OCO-2 data in growing seasons[J]. Journal of Environmental Management, 2019, 244(8): 110-118. |
| [36] |
SUN A Y, TANG G. Downscaling satellite and reanalysis precipitation products using attention-based deep convolutional neural nets[J]. Frontiers in Water, 2020, 2(11): 536743. |
| [37] |
BREIMAN L. Random forests[J]. Machine Learning, 2001, 45: 5-32. DOI:10.1023/A:1010933404324 |
| [38] |
BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24: 123-140. |
| [39] |
HO T K. The random subspace method for constructing decision forests[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(8): 832-844. DOI:10.1109/34.709601 |
| [40] |
TARKO A M, USATYUK V V. Simulation of the global biogeochemical carbon cycle with account for its seasonal dynamics and analysis of variations in atmospheric CO2 concentrations[C]//Doklady Earth Sciences. Springer Nature BV, 2013, 448(2): 258.
|
| [41] |
BIE N, LEI L, HE Z, et al. Specific patterns of XCO2 observed by GOSAT during 2009—2016 and assessed with model simulations over China[J]. Science China Earth Sciences, 2020, 63(3): 384-394. DOI:10.1007/s11430-018-9377-7 |
| [42] |
LV Z, SHI Y, ZANG S, et al. Spatial and temporal variations of atmospheric CO2 concentration in China and its influencing factors[J]. Atmosphere, 2020, 11(3): 231. DOI:10.3390/atmos11030231 |
 2024, Vol. 16
2024, Vol. 16 