2. 江苏省太湖水质监测中心站,江苏 南京 210019;
3. 南京尚清环境技术有限公司,江苏 南京 210022;
4. 南京水利科学研究院,水文水资源及水利工程科学国家重点实验室,江苏 南京 210029
2. Taihu Water Quality Monitoring Center Station, Nanjing, Jiangsu 210019, China;
3. Nanjing Shangqing Environmental Technology Co., Ltd., Nanjing, Jiangsu 210022, China;
4. Hydrology and Water Resource Department, Nanjing Hydraulic Research Institute, Nanjing, Jiangsu 210029, China
水体流动是河湖生态系统演变的重要驱动力[1],水系连通调控可以通过提升水体流动性,维系或重塑不同水体之间的水力联系和物质循环,增加水体自净能力[2]。近年来,调水工作逐渐成为了改善水环境的辅助措施[3-6],在日本隅田川[7],德国鲁尔河[8],中国太湖[9]、金银湖[10]、鄱阳湖[11]等水域均进行了实践。环境领域在水系联通性对河湖水生态演变机理的研究和实践,促进了人类对河湖生态系统演变的定量理解和认识,奠定了水生态环境调控、水系关系优化调整的重要研究基础。因此,对基流连通水平、水质现状、水环境主要影响因子进行分析和评价,有助于厘清水环境与连通性的响应关系,进一步提升调水工程的环境改善效果。
河网连通性定量研究方面主要基于水系拓扑网络结构,近年来评价方法有水文和水利学模型(水力连通性)、图论连通度理论(结构连通性)、复杂网络理论等[12-16],其中基于图论连通度理论的研究广泛应用在河道滩区、城市河网以及平原河网区的水系连通性评价、河流健康评价以及水系规划中[17-24]。水质评价和分析方法主要包括单因子污染指数法、模糊综合评价法、主成分分析法及综合水质标识指数(WQI)、内梅罗污染指数法、人工神经网络(ANNs)法等[25-30]。相较于WQI法和内梅罗污染指数法,模糊综合评价法通过建立各级水质类别的隶属矩阵,得出了对应水体的综合水质类别,判定主要影响因子。因此,模糊综合评价法能实现对各水质指标对水质影响的客观评价[31-32]。
本研究以太湖流域杭嘉湖平原跃进联圩为研究对象,利用图论连通度理论分析圩内基流连通性的空间差异及变化特性。同时展开引调水实验,结合模糊综合评价法,探索圩内水环境和水系连通性的响应关系,以期为圩区调水工作提供科学依据。
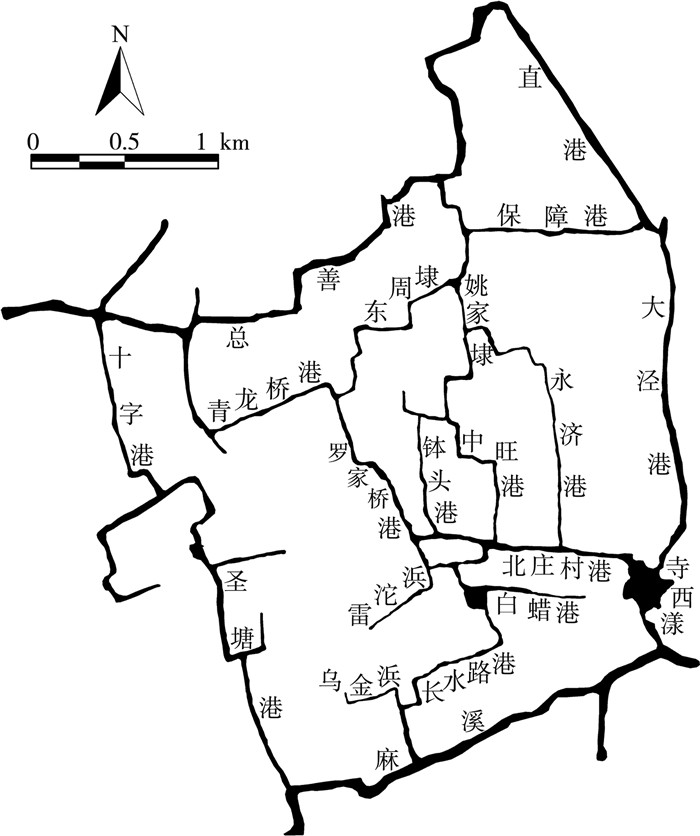
1 研究区域概况跃进联圩位于太湖流域杭嘉湖平原,行政隶属于苏州市吴江区,总面积为6.57 km2,圩内共有河道14条,总长度约1.39 km,河网密度为0.21 km/km2。圩堤将圩内外分割形成相对封闭的水文单元,目前圩内外水文循环主要通过泵站和涵闸进行水量交换,圩内水体流动性较差,圩外水质总体优于圩内。研究区域位置和水系结构示意见图 1。
|
图 1 研究区域位置和水系结构示意 |
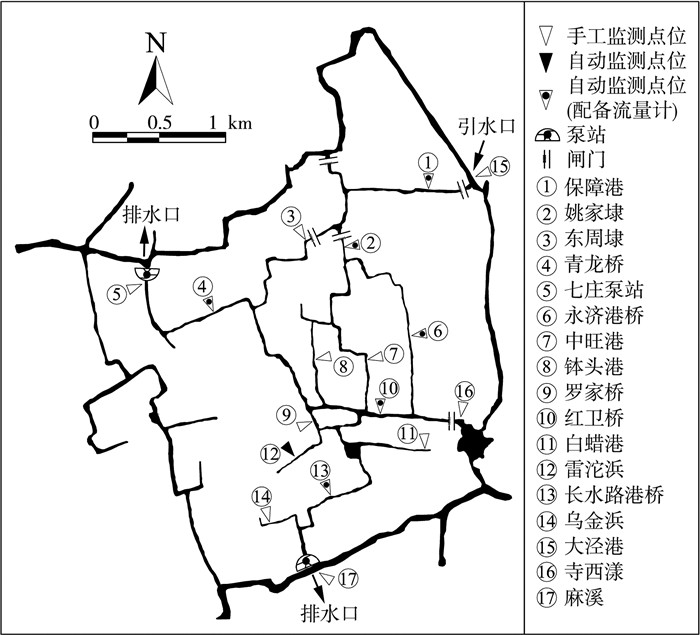
本实验共设计了3次引调水,基于水质监测数据和流量数据的变化开展研究。跃进联圩引调水试验方案见表 1。主要开启保障港东闸进行引水,期间圩内周家闸与姚家闸保持正常开启状态。试验共布设15个水质监测点位,其中6个点位设有流量监测装置(图 2)。水质监测指标包括水温、pH值、溶解氧、电导率、浊度、高锰酸盐指数、氨氮和总磷,流量监测站点监测指标包括水位和流量。
| 表 1 跃进联圩引调水试验方案 |
|
图 2 跃进联圩引调水路线及水质监测点位 |
本研究基于圩区遥感影像、气象数据、水利工程数据及水质监测数据,设计开展调水试验,分析方法主要包括图论连通度理论、单因子污染指数法以及模糊综合评价法等。利用Excel、ArcGIS、Python、Origin等软件进行数据分析及可视化处理。
3.1 图论连通度理论选取点率β、网络复杂度α和实际连通度γ来评价河流结构的连通性,将河流交汇点作为结点,2个结点之间的河道作为河链,计算公式如下:
| $ \beta=L_e / N $ | (1) |
| $ \alpha=L_e-N+p / 2 N-5 p $ | (2) |
| $ \gamma=L_e /[3(N-2 p)] $ | (3) |
式中:β——河网中河链数量与结点数量的比值,可反映每个结点平均所连河链的数量,β<1时,水系为树状结构,β>1时,水系为格状结构或回路结构;Le——河网中河链数量;N——河网中结点的数量;p——区域内分组个数;α——水流对路线可选择程度,以反映网络复杂度,α=0时,网络中没有形成回路,α=1时,网络中已达到最大限度回路数;γ——河网中实际连接线数和最大可能连接线数比值,可反映实际连通度,γ越接近1时,表明各节点间联通度越高[19-20, 33]。
3.2 模糊综合评价模型 3.2.1 模型构建模糊综合评价法是通过计算各个水质指标的污染指数并进行某种加权平均,再结合模糊数学理论计算出表征污染状态的概率,最后根据该概率值对水体水质分级评价[34-36]。
设参与评价的水环境指标因素为U =[U1 U2 U3…Um],m为参与评价的因子个数,U是一个模糊向量;设参与评价的水质指标对应的评价标准的矩阵为V =[V1 V2 V3…Vm]。
本研究选取了溶解氧、高锰酸盐指数、氨氮和总磷作为水质评价指标,分别记为U1、U2、U3、U4,根据《地表水环境质量标准》(GB 3838—2002),地表水质评价标准分为Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ共计5类,将其记为V1、V2、V3、V4、V5,模糊关系用矩阵R表示:
| $ \boldsymbol{R}=\left[\begin{array}{lllll} r_{11} & r_{12} & r_{13} & r_{14} & r_{15} \\ r_{21} & r_{22} & r_{23} & r_{24} & r_{25} \\ r_{31} & r_{32} & r_{33} & r_{34} & r_{35} \\ r_{41} & r_{42} & r_{43} & r_{44} & r_{45} \end{array}\right] $ | (4) |
式中:rij——第i种参与评价的水质指标被定为第j种水质类别的概率,即为水质指标i对水质类别j的隶属度。
将U做归一化处理后可以得到其权重矩阵A,再将A和R计算得到矩阵B,通过对比矩阵B和标准矩阵V可确定水体的水质等级。矩阵B的表达式如下:
| $ \boldsymbol{B}=\boldsymbol{A} \times \boldsymbol{R} $ | (5) |
评价标准的矩阵V中,将水环境质量标准分为n级,水质评价指标的实测值相对于各个等级水质标准的隶属度采用“半降梯形分步法”计算,隶属度rij越大,表示该因子评价指标属于该水质等级的概率就越大[37-38]。计算方法如下:
(1) 第1级(首级)水环境质量(j=1)隶属度函数
| $ r_{i 1}= \begin{cases}1, & x_i<s_{i 1} \\ \frac{s_{i 2}-x_i}{s_{i 2}-s_{i 1}}, & s_{i 1} \leqslant x_i \leqslant s_{i 2} \\ 0, & x_i>s_{i 2}\end{cases} $ | (6) |
(2) 第j级(1<j<n,中间级)水环境质量(j=2,3,…,n-1)隶属度函数
| $ r_{i j}= \begin{cases}0, & x_i<s_{i, j-1} \text { 或 } x_i>s_{i, j+1} \\ \frac{x_i-s_{i, j-1}}{s_{i j}-s_{i, j-1}}, & s_{i, j-1} \leqslant x_i \leqslant s_{i j} \\ \frac{s_{i, j+1}-x_i}{s_{i, j+1}-s_{i j}}, & s_{i j} \leqslant x_i \leqslant s_{i, j+1}\end{cases} $ | (7) |
(3) 第n级(末级)水环境质量(j=n)隶属度函数
| $ r_{i n}= \begin{cases}0, & x_i<s_{i, n-1} \\ \frac{x_i-s_{i, n-1}}{s_{i n}-s_{i, n-1}}, & s_{i, n-1} \leqslant x_i \leqslant s_{i n} \\ 1, & x_i>s_{i n}\end{cases} $ | (8) |
式中:xi——评价因子i的实测值;si,j-1、si,j、si,j+1分别为第i项因子对应的第j-1、j、j+1级水质类别标准。针对水质与数值呈正相关的评价因子,例如溶解氧,隶属度计算函数需要做相应的处理才能够使用[39]。
3.2.3 权重因子为平衡不同水质评价指标对水体水质综合评价的影响,同时体现其对水体污染情况的贡献水平,须为每个参与评价的水质指标赋予不同权重。对于水体污染物而言,该污染物实测浓度越大,对水体的污染就越重,对理想状态的隶属度就越小,就需要赋予较大的权重,反之,赋予较小的权重,但对溶解氧指标则相反[39-40]。模糊综合评价法一般采用超标加权法来计算各个指标的权重,计算方式如下:
| $ \left\{\begin{array}{l} w_{k i}=\frac{x_{k i}}{s_i} \\ s_i=\frac{1}{n}\left(c_{i 1}+c_{i 2}+\cdots+c_{i n}\right) \\ a_{k i}=\frac{w_{k i}}{\sum_{i=1}^n w_{k i}} \end{array}\right. $ | (9) |
式中:wki——第k组样品第i个指标的权重因子;xki——第k组样品第i个指标的实测值;si——第i个指标各级水质类别标准值的平均值;n——水质类别分级数量;ci——第i个指标各级水质类别标的标准值;aki——第k组样品第i个指标的归一化权重。
将所有指标的归一化权重aki组成权重矩阵A =[ak1 ak2 ak3…akn]。
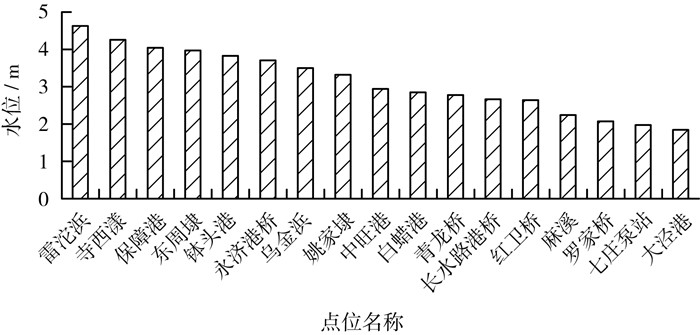
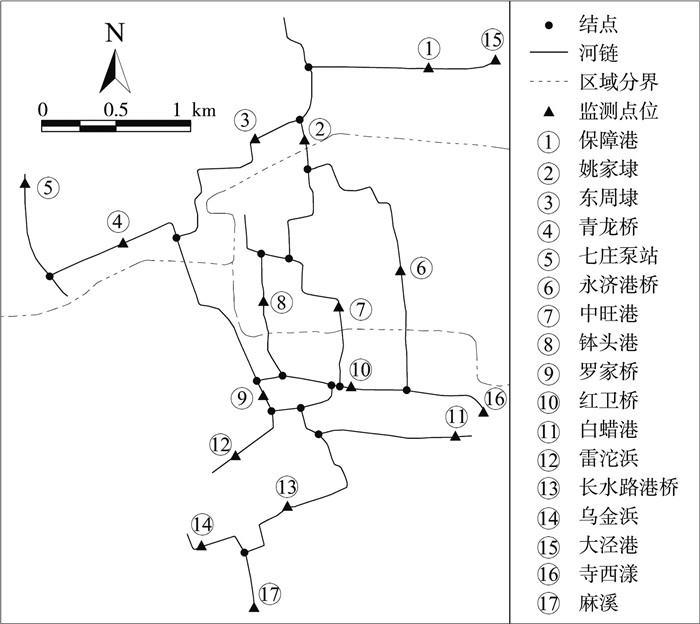
4 结果与讨论 4.1 生态基流静态连通性分析3次调水实验测试中主要引水闸门为保障港,排水泵站为七庄泵站和麻溪,结合点位水位数据(图 3),在引调水期间,圩内水体主要有2个流向,一是圩北部路线:保障港→东周埭→青龙桥→七庄泵站;二是圩南部路线:保障港→姚家埭→中旺港(钵头港)→红卫桥→长水路港桥→麻溪。结合圩内河道分布情况,将圩区基流分为北部水系、中部水系和南部水系(图 4),各区域内分组个数p为1,北部水系河链Le及结点数量N分别为3和4,中部水系河链Le及结点数量N分别为2和3,南部水系河链Le及结点数量N均为9,圩内各区域水系的点率β、网络复杂度α、实际连通度γ计算结果见表 2。此外,河宽、水深也会影响流通难易程度,本研究选取过流断面面积作为评估流通难易度的指标,过流断面面积越大,水流通过的能力就越强,跃进联圩各断面过流面积见表 3。
|
图 3 各监测点位水位情况 |
|
图 4 跃进联圩水网河链、结点及水质监测点位示意 |
| 表 2 水系连通性计算参数及结果 |
| 表 3 跃进联圩各断面过流面积 |
由表 2可见,北部和中部的水系点率β分别为0.75和0.67,为树状结构水系,南部水系点率β为1,为格状结构水系;北部、中部和南部的网络复杂度α均<1,即圩内未形成回路,总体河网结构简单;根据连通度指数γ,中部水系连通度最高,其次为北部水系,南部水系连通度最低。根据过流面积结果(表 3),北部、中部、南部水系过流面积平均值分别为52.1,33.6和26.5 m2,即相较于中部和南部水系,北部水系河道具备最高的过水能力。此外,根据3次引调水期间圩内各点位流速平均值显示(图 5),南部水系红卫桥流速最低,长水陆港桥靠近南部麻溪排水泵站,流速相较于红卫桥有所提高,但仍低于中部水系和北部水系;北部水系的保障港位于引水口,流速明显高于圩内其他点位,靠近七庄排水泵站的青龙桥流速也处于较高水平;中部水系的永记港流速仅次于保障港;姚家埭处河道变宽,流速有所下降。

|
图 5 研究区各点位流速平均值 |
引调水期间圩内流速整体上呈现由北向南逐渐降低的趋势。因此,即使南部麻溪泵站处于开启状态,由保障港引入的圩外水源仍然多从北部水系通过。
4.2 水质分析调水期间基于单因子污染指数法的水质评价结果见图 6(a)—(h)。由图 6可见,圩外水质相对比较稳定,引水水源水质没有明显优于圩区内。调水期间北部区域东周埭、姚家埭、青龙桥水质有好转趋势,但圩内整体水质改善不明显,水质类别上升幅度不大。

|
图 6 调水期间基于单因子指数法的水质评价结果 |
相较于单因子法,模糊评价法可以更加清晰地显示圩内各监测点位水质的变化情况,具体见图 7(a)—(h)。由图 7可见,引调水期间圩内水质类别Ⅰ类,Ⅱ类,Ⅲ类,Ⅳ类和Ⅴ类的占比分别为8.9%,25.0%,32.1%,25.9%和8.1%,水质类别Ⅲ类及以上的比例达到66%。
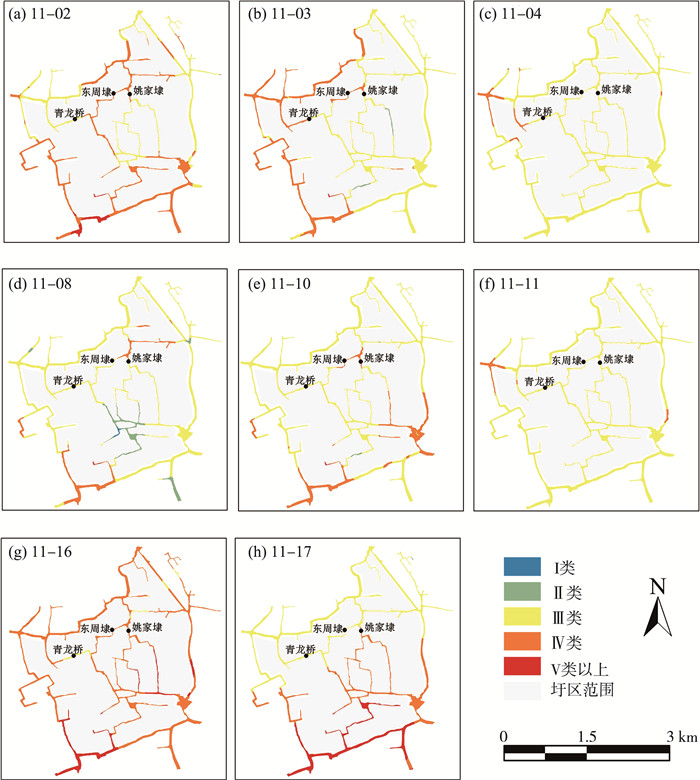
|
图 7 调水期间基于模糊评价法的水质评价结果 |
结合生态基流静态分区,北部和中部水系连通性优于南部水系,调水期间水质水平与连通性呈正相关,南部水质基本处于Ⅳ—Ⅴ类水平。引调水期间对水质的隶属度和权重的因素贡献水平见图 8。其中北部区域主要受溶解氧因子影响,中部水系环境复杂,受到氨氮、高锰酸盐指数和溶解氧的影响。南部区域水环境主要影响因子为高锰酸盐指数和溶解氧。综合来看,高锰酸盐指数对Ⅴ类水质区域的隶属度和权重最高,即高锰酸盐指数是圩内水质恶化的主要影响因素。
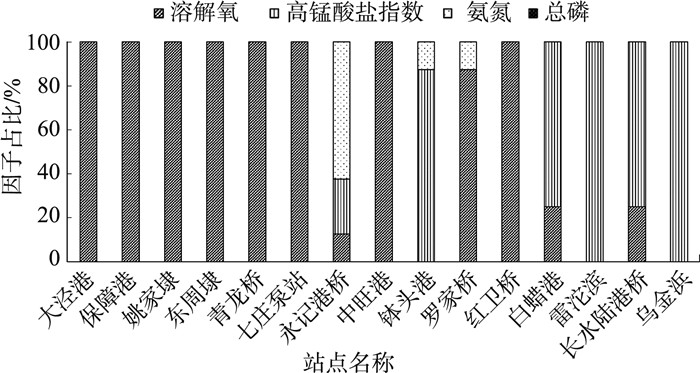
|
图 8 引调水期间对水质的隶属度和权重的因素贡献水平 |
结合水体实际流动性和引调水试验设计,前2次调水持续时间为48 h,闸门开度为10 cm,第3次持续24 h,闸门开度20 cm,即3次累计调水总量基本一致。第1次引调水后,圩内总体水质呈现持续改善趋势,在调水结束后的第4 d达到最优水平。第2次引调水对基流连通性较好的北部和中部区域有明显的水质改善作用,其中,永记港桥受河道施工截流影响,流动性变差,水质下降明显。第3次引调水仅开启了北部七庄排水泵站,在南部无排水口的情况下,圩内水量更多从北部水系流通,故圩内除北部区域外,其他区域水质未见明显改善,临近南部麻溪排水泵站的长水陆桥和乌金浜区域水体流动性明显变差,水质出现了明显的下降。综上,在调水总量一致的情况下,引排水口数量会直接影响圩内各区域水体的流动性,从而影响该区域引水的过流量,最终决定了引调水工程对环境的改善效果,即水体流动性越好,引水过流量越大,水质改善情况越明显。
5 结论(1) 模糊综合评价法在引调水环境改善分析中具有适用性。相较于单因子污染指数法,模糊综合评价法可以更加清晰地显示圩内各监测点位水质的变化情况,有助于全面分析引调水工程对圩区内水质改善的情况。
(2) 水体流动性是影响圩内水质的重要环境因素。引调水工程是增加圩区水体流动性的有效方式,水体流动性越好,引水过流量越大,水质改善情况越明显。
(3) 引调水工程对圩区水环境具有持续改善性作用。定期开展引调水工程可以改善圩区水质,但对基流连通性较差的区域,改善效果有限。
(4) 高锰酸盐指数是圩内水质恶化的主要影响因素。建议后期开展圩内水体有机物及可氧化无机物溯源调查,并采取一定防范及治理措施,进一步提升圩内水环境质量。
| [1] |
左其亭, 崔国韬. 河湖水系连通理论体系框架研究[J]. 水电能源科学, 2012, 30(1): 1-5. |
| [2] |
王中根, 李宗礼, 刘昌明, 等. 河湖水系连通的理论探讨[J]. 自然资源学报, 2011, 26(3): 523-529. |
| [3] |
于珊, 李一平, 程一鑫, 等. 调水引流工程对平原河网水动力调控的效果[J]. 湖泊科学, 2021, 33(2): 462-473. |
| [4] |
王焕雄. 福州市光明港二支河水动力优化成效分析[J]. 陕西水利, 2022(7): 101-103, 106. |
| [5] |
魏清福. 平原河网圩区水利工程生态调度方案研究--以苏州吴中城南包围为例[J]. 人民长江, 2022, 53(10): 31-36. |
| [6] |
崔广柏, 陈星, 向龙, 等. 平原河网区水系连通改善水环境效果评估[J]. 水利学报, 2017, 48(12): 1429-1437. |
| [7] |
汤建中, 宋韬, 江心英, 等. 城市河流污染治理的国际经验[J]. 世界地理研究, 1998(2): 114-119. |
| [8] |
BODE H, EVERS P, ALBRECHT R D, et al. Integrated water resources management in the Ruhr River Basin, Germany[C]. Proceedings of the 3rd World Water Congress: Integrated Water Resources Management. 2003.
|
| [9] |
黄春琳, 李熙, 孙永远. 太湖水龄分布特征及"引江济太"工程对其的影响[J]. 湖泊科学, 2017, 29(1): 22-31. |
| [10] |
瞿春梅, 乔书娜, 刘伯娟, 等. 基于水质改善的湖泊引调水数值模拟研究--以武汉市金银湖为例[J]. 三峡生态环境监测, 2019, 4(4): 9-17. |
| [11] |
赖格英, 王鹏, 黄小兰, 等. 鄱阳湖水利枢纽工程对鄱阳湖水文水动力影响的模拟[J]. 湖泊科学, 2015, 27(1): 128-140. |
| [12] |
徐祖信. 我国河流综合水质标识指数评价方法研究[J]. 同济大学学报(自然科学版), 2005, 33(4): 482-488. |
| [13] |
李如忠. 水质评价理论模式研究进展及趋势分析[J]. 合肥工业大学学报(自然科学版), 2005, 28(4): 369-373. |
| [14] |
李经伟, 杨路华, 梁宝成, 等. 改进的主成分分析法在白洋淀水质评价中的应用[J]. 海河水利, 2007(3): 40-43. |
| [15] |
PESCE S F, WUNDERLIN D A. Use of water quality indices to verify the impact of Córdoba City(Argentina) on Suqua River[J]. Water Research, 2000, 34(11): 2915-2926. DOI:10.1016/S0043-1354(00)00036-1 |
| [16] |
耿慧, 谢建治, 刘树庆. 水质标识指数法在白洋淀水质评价中的应用[J]. 河北农业大学学报, 2011, 34(3): 93-98. |
| [17] |
徐俊明. 图论及其应用[M]. 合肥: 中国科学技术大学出版社, 2004.
|
| [18] |
危小建, 江平, 陈竹安, 等. 基于拓扑结构和空间网络结构的水系连通性评价[J]. 人民长江, 2019, 50(5): 76-81. |
| [19] |
王云才. 上海市城市景观生态网络连接度评[J]. 地理研究, 2009, 28(2): 284-292. |
| [20] |
沈洁. 上海浦东新区城市化进程对水系结构、连通性及其调蓄能力的影响研究[D]. 上海: 华东师范大学, 2015.
|
| [21] |
赵进勇, 董哲仁, 翟正丽, 等. 基于图论的河道-滩区系统连通性评价方法[J]. 水利学报, 2011, 42(5): 537-543. |
| [22] |
马爽爽. 基于河流健康的水系格局与连通性研究[D]. 南京: 南京大学, 2013.
|
| [23] |
邓晓军, 许有鹏, 翟禄新, 等. 城市河流健康评价指标体系构建及其应用[J]. 生态学报, 2014, 34(4): 993-1001. |
| [24] |
孟慧芳, 许有鹏, 徐光来, 等. 平原河网区河流连通性评价研究[J]. 长江流域资源与环境, 2014, 23(5): 626-631. |
| [25] |
鄢回, 郁建桥, 徐洁, 等. 改进的模糊综合评价法在太湖水质类别判定中的应用[J]. 环境监控与预警, 2012, 4(2): 39-44. |
| [26] |
王姗姗, 张然, 梁悦, 等. 城市水质指数法在地表水环境质量评价中的应用[J]. 环境监控与预警, 2022, 14(1): 67-71. |
| [27] |
耿姣, 王洋, 胡术刚, 等. 基于WQI的平原河网地区河流水质评价与时空变化分析[J]. 环境工程, 2023, 41(6): 187-193, 209. |
| [28] |
陈雨艳, 杨媛媛, 石翔宇, 等. 基于改进的内梅罗污染指数法的茫溪河水质分析[J]. 四川环境, 2022, 41(6): 144-147. |
| [29] |
胡伟, 李晓, 侯佳均, 等. 基于BP神经网络法的平谷地下水水质评价[J]. 甘肃水利水电技术, 2020, 56(9): 13-17, 62. |
| [30] |
张进. 基于模糊综合指数法对丹江上游水质评价[J]. 陕西水利, 2022(7): 98-100, 106. |
| [31] |
李昂, 水西霞, 员佳慧, 等. 支持向量机与模糊综合指数法在水质评价中的应用[J]. 科技创新与应用, 2022, 12(10): 181-184. |
| [32] |
夏焕清, 霍秀秀. 基于模糊综合指数法的嘉陵江汉中段水质评价[J]. 陕西水利, 2020(12): 96-99. |
| [33] |
赵军. 平原河网地区景观格局变化与多尺度环境响应研究[D]. 上海: 华东师范大学, 2008.
|
| [34] |
LI L, ZHOU J, AN X, et al. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China[J]. Expert Systems with Applications, 2010, 37(3): 2517-2521. DOI:10.1016/j.eswa.2009.08.004 |
| [35] |
DAHIYA S, SINGH B, GAUR S, et al. Analysis of groundwater quality using fuzzy synthetic evaluation[J]. Journal of Hazardous Materials, 2007, 147(3): 938-946. DOI:10.1016/j.jhazmat.2007.01.119 |
| [36] |
李茜茜. 沁河流域晋城段水质评价及影响因素分析[D]. 山西: 山西财经大学, 2019.
|
| [37] |
关磊声. 大同口泉沟-云冈沟矿区煤矿采空区水水质评价[D]. 安徽: 安徽理工大学, 2019.
|
| [38] |
LU X, LI L Y, LEI K, et al. Water quality assessment of Wei River, China using fuzzy synthetic evaluation[J]. Environmental Geology, 2010, 60(8): 1693-1699. |
| [39] |
郑艺. 基于模糊数学方法的水质综合评价[J]. 治淮, 2015(1): 16-17. |
| [40] |
杨日剑. 典型村镇水质评价与预测方法研究及应用[D]. 长沙: 湖南大学, 2016.
|
 2024, Vol. 16
2024, Vol. 16 

