总β是指样品中最大能量>0.3 MeV的不挥发的β辐射粒子[1]。大部分的人工放射性核素可能放射出β粒子,因此能够通过测定气溶胶中的总β放射性来了解核电监督性监测区域空气的放射性状况。总β的检测简单快速,成本低,所以在环境放射性评价中被大量采用。这对积累空气中辐射水平监测数据,研究空气中辐射水平变化规律以及判断环境放射性污染程度具有重要意义[2-3]。当前气溶胶和沉降物中总β监测已成为大多数核设施的常规监测项目[4]。
福清核电厂建有6台百万千瓦级压水堆核电机组,核电厂的运营对周边大气环境是否存在放射性影响,不仅是监管部门重点关注的问题,也是核电厂周边群众最为关心的问题。因此,为探究核电厂运行近10年来对周边大气环境的放射性影响情况,有必要对核电厂周边大气环境放射性监测数据进行统计学分析,并与国内外类似核电厂的监测数据进行比对分析,利用相关数学模型,评价其变化趋势及规律,为核电厂大气流出物排放进行预警性提示,也为国内类似核电厂开展监测数据分析提供经验参考。
1 研究材料与方法 1.1 研究区概况福建福清核电厂位于福建省福清市三山镇前薛村,北、南、西三面环海,东北侧与陆地连接。厂址区域属典型的亚热带海洋性季风气候,当地受季风和海风的影响明显,冬、夏季风方向随季节交替而转换,风速自沿海向平原及内地山区减弱。代表性气象站观测的当地年平均温度为19.8 ℃,年均相对湿度为80%,最小相对湿度为12%。厂址区域大气稳定度为中性(帕斯奎尔法,D类)的占绝对优势,强不稳定性(A类)所占比例最少。由于厂址地处沿海,常年风速较大,从稳定度的分类和风速的结果可以判断当地的大气弥散条件较好,有利于气载污染物的扩散。
1.2 气溶胶采样与监测分析方法根据国家辐射环境监管的要求,福建省辐射环境监督站从2015年开始,对福清核电厂周边环境展开监督性监测。福清核电厂气态监督性监测设有3个监测取样点和1个对照取样点,监督性监测点位及2015—2022年前薛站风向风频图见图 1。福州市福飞北路对照点距离核电厂约80 km。
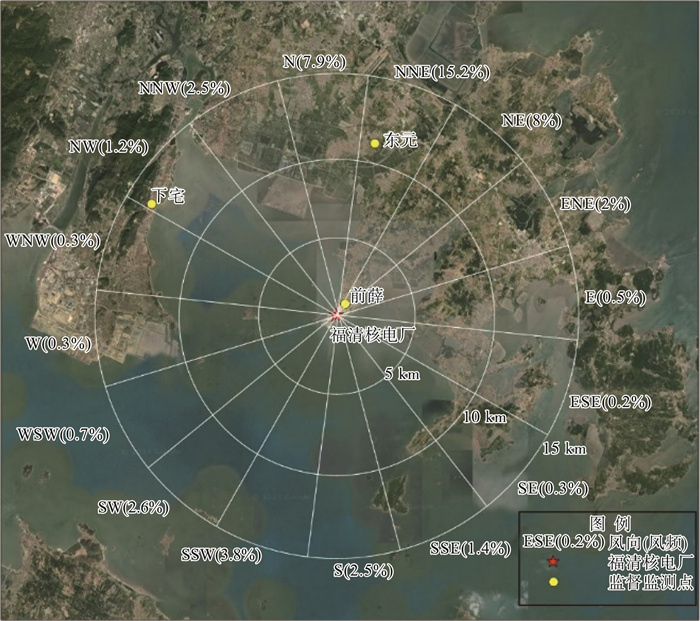
|
图 1 监督性监测点位及2015—2022年前薛站风向风频图 |
监测分析方法:采用灰化法测量气溶胶中总β放射性[5]。
统计学方法:用SPSS 27进行统计分析,因样本数>50,数据的正态性检验采用K-S法[6]。经正态性检验发现,东元、下宅监测点位总β值符合正态分布(P值分别为0.075和0.200),前薛、福州对照点不符合正态分布(P值分别为0.033和0.038),故2个独立样本的比较用斯皮尔曼(Spearman)秩相关系数进行相关性分析,检验水平α=0.05。
数学建模方法:整合移动平均自回归模型(ARIMA)是时间序列分析的重要方法之一[7-8],时间序列时域分析方法从自相关的角度揭示时间序列的发展规律[9]。ARIMA模型允许序列中含有趋势变动、季节性变动等因素的影响[10]。建模步骤:平稳性检验→平稳化处理与检验→模型定阶及参数估计→残差检验[11]。
2 结果与讨论 2.1 监测结果分析2015—2022年福清核电厂各监测点位气溶胶中总β活度浓度监测结果统计见表 1。由表 1可见,前薛、东元、下宅3个监测点位总β活度浓度平均值为0.808~0.816 mBq/m3,平均值变化范围很小,说明福清核电厂周边气溶胶中总β的放射性水平相近。各监测点位总β活度浓度的标准偏差与平均值的比值都较大,说明总β的监测数值较离散,这与核电厂地处沿海,大气弥散条件较好有关。对照点的总β活度浓度平均值为0.957 mBq/m3,高于核电厂周边监测点位数值。究其原因可能与福飞北路监测点地处城市,来自城市的放射性污染源(医院、工业生产、垃圾焚烧厂、汽车尾气等)较多有关。尤其与对照点距离较近(3.5 km)的红庙岭垃圾焚烧厂,在一定程度上提高了对照点监测数值。另外,福州市区地处盆地,四面环山,对于气载污染物的扩散极为不利,也对提高对照点的放射性水平有一定的贡献。
| 表 1 2015—2022年福清核电厂各监测点位气溶胶中总β活度浓度监测结果统计 |
对3个监测点位及福州对照点监测数据进行一致性分析,监测点位间配对总β的Spearman相关系数见表 2。由表 2可见,福州对照点与核电厂周边监测点位的监测数据在统计学上无显著性差异(显著性 < 0.001)。福州对照点与核电厂周边3个监测点间的Spearman秩相关系数(P值)约为0.550,核电厂周边3个监测点位间的P值在0.870左右,因此可以认为前薛、东元、下宅站点间有更紧密的相关性。
| 表 2 监测点位间配对总β的Spearman相关系数 |
刘鸿诗等[12]报道了秦山核电厂周边气溶胶中总β活度浓度为0.100~1.810 mBq/m3,甄丽颖等[13]报道了阳江核电厂外围气溶胶总β活度浓度为0.050~2.460 mBq/m3。本研究统计了福建省宁德核电厂总β监测数据,整理了同位于大洋西岸,处于相同纬度,同为压水堆的美国佛罗里达州的土尔其角(Turkey Point)核电厂3,4号机组于2011—2021年的总β环境监测数据[14],结果见表 3。由表 3可见,福建省2座核电厂总β均值高出国内其他地区1.34~1.77倍,分析原因可能是福建地区土壤中天然放射性核素238U、232Th、226Ra较全国水平偏高,在正常工况下,受扬尘影响,气溶胶中总β监测值偏高[15]。秦山核电厂及美国土尔其角核电厂气态流出物总β归一化后数值较小[<0.1(mBq/m3)/kMWe],其他3座核电厂归一化后数值稍大[>0.1(mBq/m3)/kMWe],秦山核电厂(1991年运行)和土尔其角核电厂(1967年运行)运行时间较长,而其他3座核电厂运行时间较短,均未超过10年。核电厂运行时间的长短对其周边总β监测值会带来怎样的影响,目前国内还没有相关的文献记载,有待进一步分析研究。
| 表 3 国内外核电厂气溶胶中监测数据统计 |
根据3个监测点采集的2016年5月—2022年12月的降雨量信息,分析降雨量与气溶胶中总β放射性水平的关系。考虑核电厂可能存在的集中排放,采用月降雨量信息,计算3个站点的总β与降雨量的P值,在不相关假设条件下,P值(P前薛=0.038,P东元=0.031,P下宅=0.012)均<0.05,故拒绝原假设,3个站点的总β监测值都与降雨量相关。P值分别为-0.234,-0.251,-0.285,表现为负相关性。进一步作总β监测值—降雨量线性回归拟合图进行验证,结果见图 2(a)—(c)。
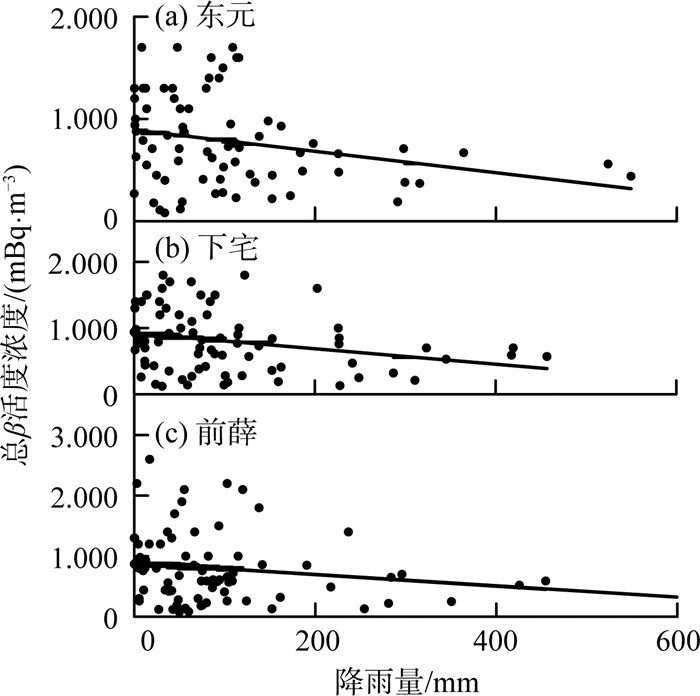
|
图 2 3个采样点位总β监测值—降雨量直线拟合 |
由图 2可见,前薛、东元、下宅3个点位弃真概率P值分别为0.099,0.026,0.019,东元和下宅P值<0.05,具有统计学意义。综合分析,可以认为随着降雨量的增加,核电厂周边气溶胶中总β监测值呈缓慢下降趋势。这与甄丽颖等[13]报道的阳江核电厂气溶胶中总β与降雨量的关系一致。
2.4 总β活度浓度逐月分析为了明确总β活度浓度在一年中随月份变化的情况,对92个月的整体数据进行统计分析。福清核电厂和美国土尔其角核电厂气溶胶总β监测值>平均值的占比月度分布见图 3(a)(b)。
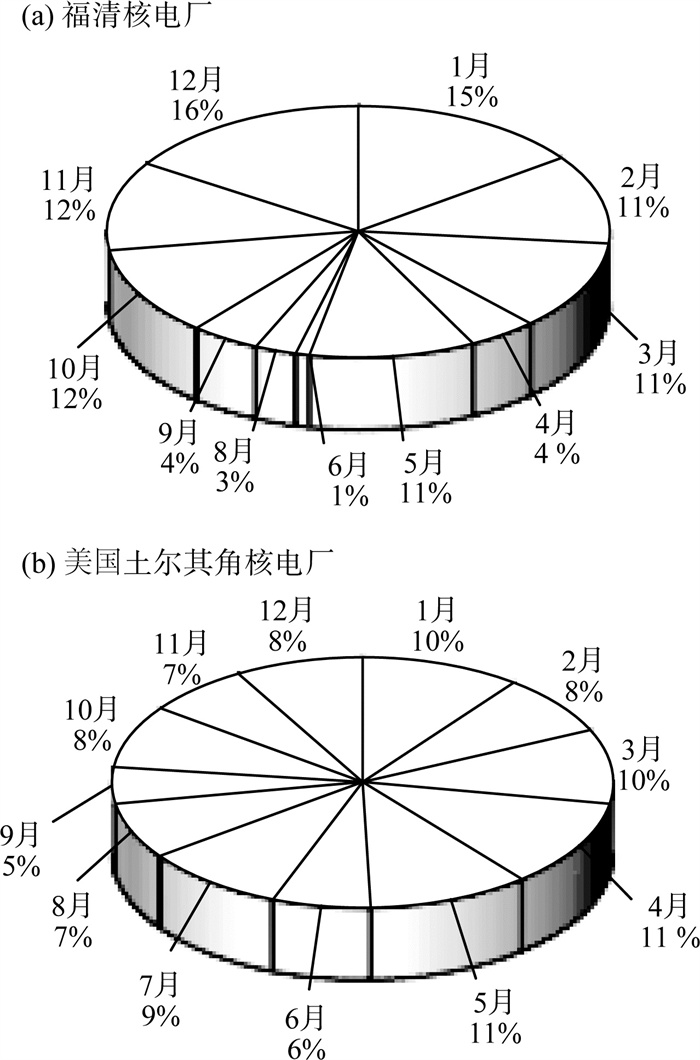
|
图 3 福清核电厂和美国土尔其角核电厂气溶胶总β监测值>平均值的占比月度分布 |
由图 3(a)可见,总β监测值>平均值的样本量主要集中在10,11,12,1月,这4个月占比之和为55%,其余8个月每月占比呈随机分布,占比数值均较小,8个月占比总和为45%。甄丽颖等[13]报道的阳江核电厂周边大气中总β活度浓度最高值出现在冬、春季,陈彬等[16]报道的秦山核电厂周边大气气溶胶总β放射性数据较高的月份主要集中在10月至次年1月,吉长余等[17]报道了大亚湾核电厂周围大气总β活度浓度冬、春季高于夏、秋季。福清核电厂的气溶胶总β活度浓度月份分布情况与上述核电厂基本一致。由图 3(b)可见,相较于福清核电厂,美国土尔其角核电厂总β活度浓度的月份分布情况更加均衡,总β监测值>平均值的月份占比为5%~11%,没有明显的季节性。
3 总β活度浓度ARIMA模型的构建与优化为探究总β活度浓度随时间变化的规律,并预测未来短期的走势,本研究利用长期监测数据进行时间序列分析,建立并优化总β活度浓度的ARIMA模型。选择84个月(2016年1月—2022年12月)样本数据进行统计分析,对总β活度浓度数据作原始时间序列图。总β活度浓度月平均值原始时间序列自相关(ACF)、偏自相关(PACF)图见图 4(a)(b)。由图 4可见,时间序列始终在一个常数值附近随机波动,但在间隔一定时段后数值会增高,没有表现为明显的趋势,但可能呈现周期性特征。ACF图后面的数据没有收敛,呈波动状态,且有较多部分在置信区间以外。PACF图呈现一阶截尾,但也有较多部分处在置信区间以外。故初步判定总β活度浓度原始时间序列为一个非平稳时间序列。
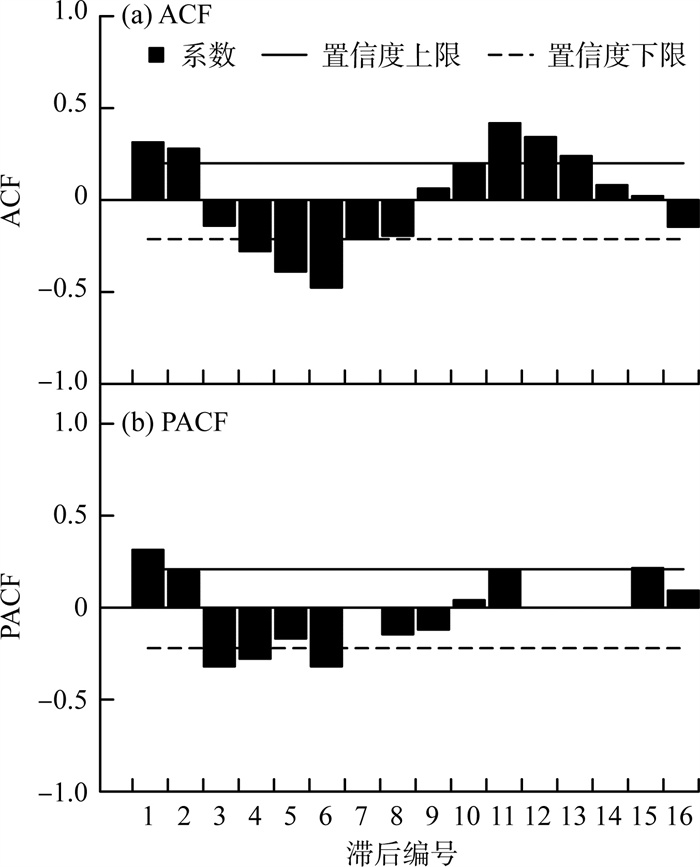
|
图 4 总β活度浓度月平均值原始时间序列ACF、PACF图 |
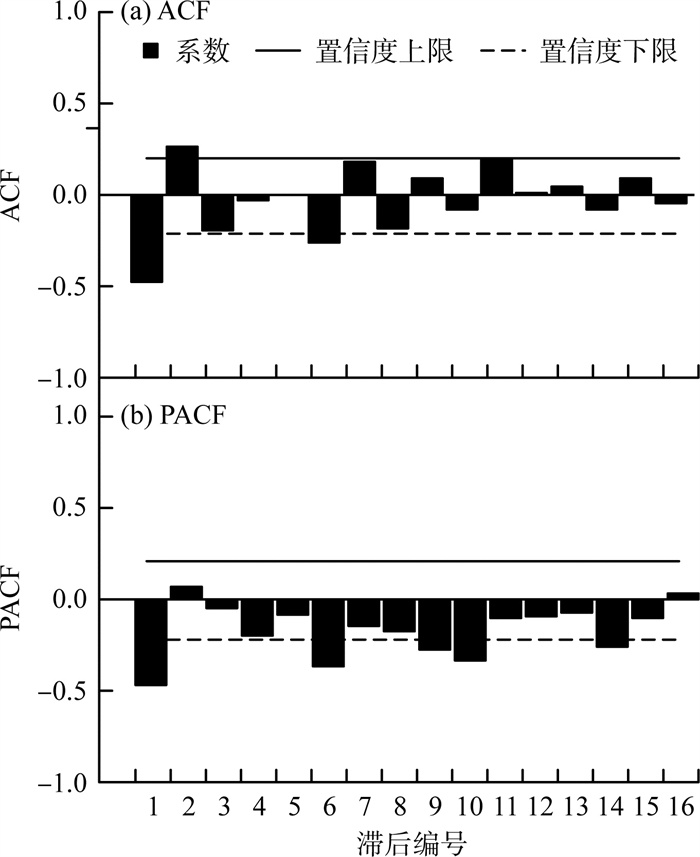
对总β活度浓度原始时间序列进行1阶差分。1阶差分序列ACF、PACF图见图 5(a)(b)。由图 5可见,ACF表现为2阶截尾,PACF表现为1阶拖尾,因此1阶差分后的总β活度浓度时间序列为平稳序列,故p=2,q=1。初步判定模型为ARIMA(2,1,1)。
|
图 5 1阶差分序列ACF、PACF图 |
由2.4节分析结果可知,总β活度浓度在10月至次年1月份有所增高,冬、春季监测数值较高,表现为一定的季节性。在确定本模型的季节性参数时采取试探的方案,p、q通常选择0,1,2。在ARIMA(2,1,1)的基础上,选择10个备选模型进行参数估计。经计算,10个备选模型中有7个模型参数具有统计学意义,结果见表 4。
| 表 4 备选模型参数① |
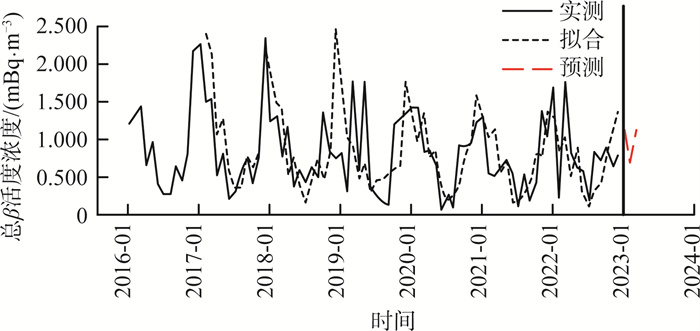
由表 4可见,7个模型中ARIMA(2,1,1)(0,1,1)的正态化BIG最小,显著性最大,并且平稳R2(0.669)在7个模型中也处于较好水平,故选定ARIMA(2,1,1)(0,1,1)为时间序列预测模型,拟合效果见图 6。根据模型输出结果,2023年第1季度(1—3月)的总β活度浓度预测值为1.293,0.679,1.126 mBq/m3。
|
图 6 总β活度浓度ARIMA(2,1,1)(0,1,1)模型拟合 |
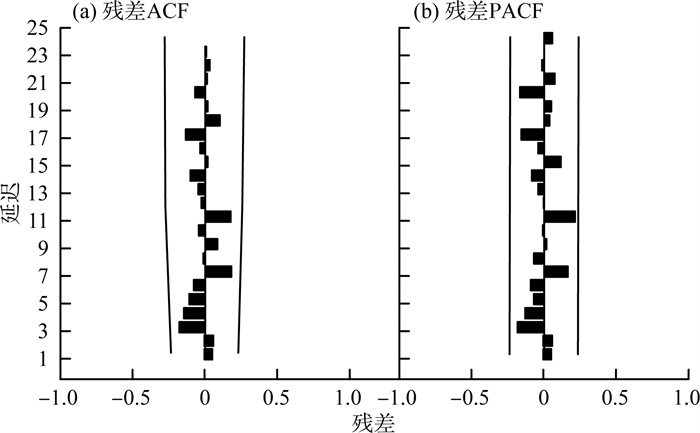
选定最终模型后,进一步采用ACF和PACF图对ARIMA(2,1,1)(0,1,1)模型残差进行白噪声检验,结果见图 7(a)(b)。由图 7可见,ACF、PACF均处在置信区间内且在0值的两侧波动,并且逐渐趋近于0。所以确定模型ARIMA(2,1,1)(0,1,1)拟合后的残差项为白噪声序列,因此不能拒绝时间序列为纯随机序列的原假设,通过检验,无须继续建模。
|
图 7 ARIMA(2,1,1)(0,1,1)模型拟合残差ACF、PACF图 |
分析拟合图发现,模型ARIMA(2,1,1)(0,1,1)总体上能够较好地拟合总β的活度浓度实测值,但对个别极值拟合效果不理想,整体拟合效果滞后。2023年1—3月实测值与预测值偏差验算结果见表 5。由表 5可见,总β活度浓度实测值与预测值的偏差分别为46.4%,5.3%,4.3%。2,3月的实测值与预测值相差不大,偏差都在5%左右,比较理想。但从历史监测数据上看,1月出现极值的概率较高,从而使得实测值与预测值的偏差较大,同时也印证了模型ARIMA(2,1,1)(0,1,1)对极值的预测还不够理想。分析原因,可能因为1月正处春节期间,烟花爆竹的燃放对核电厂周边总β活度浓度监测值的突变有着较大的影响,容易造成监测极值的出现。
| 表 5 2023年1—3月实测值与预测值偏差验算结果 |
(1) 福清核电厂监督性监测站点的总β活度浓度监测值与降雨量均表现为负相关,没有明显的季节性。
(2) 利用福清核电厂长期大气放射性监测数据,以总β活度浓度为分析对象,讨论并确定了总β时间序列的模型为ARIMA(2,1,1)(0,1,1),可对核电厂周边大气中的放射性水平进行预测,为辐射环境影响评价提供依据。模型拟合优度为0.669,对极值的预测还不够理想,仍有进一步改进的空间,可结合非线性动力学[18]和BP神经网络[19-20]等方法对模型进行优化。
(3) 福州对照点总β活度浓度的均值、偏差、最大值等统计量比核电厂周边监测点稍高,所有站点总β活度浓度测值均处于辐射环境本底水平。然而周边环境对对照点的影响较大,数据的稳定性较差,已失去低本底对照点的意义,故建议选择受人为活动影响较小的地点,如避开高温、多湿、扬尘,且易受事故、灾害影响的场所,以及受周边的环境、建筑物影响较小,距高大建筑物距离与建筑物高度比≥1,直线距离≥30 m的其他站点作为对照点。
| [1] |
环境保护部. 水质总β放射性的测定厚源法: HJ 899—2017[S]. 北京: 中国环境出版集团, 2017.
|
| [2] |
李芳, 陆继根, 沙连茂, 等. 固体中总α、总β放射性监测方法研究[J]. 辐射防护, 2007, 27(4): 228-232. |
| [3] |
赵力, 李冬梅, 周鹏, 等. 昌江核电站运营前附近海域总β放射性水平[J]. 海洋环境科学, 2021, 40(4): 521-526. |
| [4] |
刘书田, 夏益华. 环境污染监测实用手册[M]. 北京: 原子能出版社, 1997: 40-44.
|
| [5] |
王春梅. 核应急监测中气溶胶总α、总β放射性测量[J]. 能源与环境, 2021(4): 80-81. |
| [6] |
国家质量技术监督局. 数据的统计处理和解释正态性检验: GB/T 4882—2001[S]. 北京: 中国标准出版社, 2001.
|
| [7] |
王燕. 时间序列分析: 基于R[M]. 北京: 中国人民大学出版社, 2015.
|
| [8] |
HYNDMAN R J, ATHANASOPOULOS G. Forecasting: principles and practice[M]. 2nd edition.Melbourne, Australia: OT-exts, 2018.
|
| [9] |
李颖若, 韩婷婷, 汪群霞, 等. ARIMA时间序列分析模型在臭氧浓度中长期预报中的应用[J]. 环境科学, 2021, 42(7): 3118-3126. |
| [10] |
李娜, 李勇, 冯家成. 太湖水体Chl-a预测模型ARIMA的构建及应用优化[J]. 环境科学, 2021, 42(5): 2223-2231. |
| [11] |
张万里, 郑永浩, 邢万丽, 等. 基于ARIMA模型的环渤海典型城市生活垃圾产量预测研究[J]. 环境工程技术学报, 2022, 12(3): 861-868. |
| [12] |
刘鸿诗, 胡晓燕, 陈杉, 等. 秦山核电基地外围环境放射性水平20年监测结果[J]. 原子能科学技术, 2013, 47(10): 1906-1915. |
| [13] |
甄丽颖, 张家俊. 阳江核电厂外围环境气溶胶总α、总β放射性水平[J]. 核技术, 2017, 40(8): 46-50. |
| [14] |
U.S. Nuclear Regulatory Commission. Turkey point nuclear units 3 & 4 annual radiological environmental operating report(2011—2021)[R].
|
| [15] |
王春梅, 何喆, 陈永伟, 等. 2007—2011年福建省辐射环境监测[J]. 辐射防护通讯, 2015, 35(5): 43-46. |
| [16] |
陈彬, 叶际达, 吴晓飞, 等. 秦山核电基地外围环境气溶胶总α、总β放射性水平监测[J]. 辐射防护通讯, 2006, 26(5): 31-35. |
| [17] |
吉长余, 张东果. 大亚湾核电站1994~2003年环境辐射监测结果与分析[J]. 辐射防护, 2004, 24(3-4): 173-190. |
| [18] |
CHELANI A B, DEVOTTA S. Prediction of ambient carbon monoxide concentration using nonlinear time series analysis technique[J]. Transportation Research, 2007, 12(8): 596-600. |
| [19] |
胡剑波, 罗志鹏, 李峰. "碳达峰"目标下中国碳排放强度预测——基于LSTM和ARIMA-BP模型的分析[J]. 财经科学, 2022(2): 89-101. |
| [20] |
张晶晶. 基于ARIMA-BP神经网络的PM2.5组合预测[D]. 兰州: 兰州大学, 2022.
|
 2024, Vol. 16
2024, Vol. 16 