2. 生态环境部华南环境科学研究所河口与海岸生态环境研究中心,广东 广州 530535
2. South China Institute of Environmental Sciences, Ministry of Ecology and Environment, Guangzhou, Guangdong 530535, China
当前,中国水环境的富营养化、饮用水源地污染、地下水与近海海域污染等问题尚未得到根本解决,蓝藻水华、水生态失衡问题依然存在。总磷作为水体富营养化的关键影响因子,其浓度过高会导致藻类大量繁殖,破坏生态平衡。2022年生态环境部公告显示,监测的204个重要湖泊(水库)中,29.9%处于不同程度的富营养化状态。总磷浓度预测是治理地表水体磷污染的重要手段,是根治地表水体富营养化的重要措施[1]。
早期的水质预测更多的是通过判断河流的地理、物理和化学机制来对水质进行判断,代表性模型有美国环境保护局构建的QUAL、QUAL2E模型[2-3]和丹麦研究所开发的MIKE模型[4]。这些模型依赖地理位置、气象、水文等数据,难以推广。
近几年来深度学习迅速发展,长短时记忆网络(LSTM)作为经典的时间序列框架,逐渐被用于解决水质预测问题。Barzega等[5]构建了耦合深度卷积和长短时记忆(CNN-LSTM)模型预测水质变量;张贻婷等[6]使用长短时记忆网络对河流水质进行预测;Pang等[7]和马志峰等[8]也尝试使用长短时记忆网络解决短时水质预测问题。这些基于长短时记忆网络的水质预测模型,虽然在一定程度上提升了预测精度,但均未考虑水质数据的多尺度动态变化,使得模型局限于处理短时预测问题,在涉及不同月份和季节的长期预测问题上表现并不稳定。自2013年至今,以Transformer为基础的深度学习框架,在地表水预测模型方面的应用越来越广泛[9]。Yao等[10]将Transformer与经典的循环神经网络(RNN)和长短时记忆网络在水质预测问题上的性能进行了对比;Rocha等[11]将Transformer和图神经网络(GNN)结合,对天然河流的溶解氧水平进行预测;Wang等[12]使用图卷积网络(GCN)提取地理和气象特征,并利用Transformer对溶解氧浓度进行预测;Informer模型也是Transformer模型的重要变种,主要解决长期序列预测,在巢湖地区的研究中显示出显著优势[13]。这些模型均以Transfromer为基础,能够较好地解决长期依赖问题,在中长期预测方面略优于其他深度网络,然而这些研究缺乏对于数据复杂时变性的设计,致使模型结果在复杂的数据上不稳定。此外,多任务深度学习通过同时训练多个模型,显著提高了模型的时间稳定性和泛化能力[14],然而这一类综合模型对算力要求高,训练时间长,且易出现过拟合、梯度爆炸和梯度消失等问题。
本研究提出一种基于数据稳态调控和深层时序解析的模型(DSC-SDP-TF),以解决水质预测的关键难点。针对水质数据的复杂时变性,设计数据稳态调控模块(DSC),将输入序列进行稳态转换,使得用于建模的数据具有稳定的统计特性,从而增强了模型在数据上的鲁棒性。同时根据输入序列稳态变换的公式对传统注意力机制进行了改进,提升了注意力机制的性能。针对水质数据的多尺度动态变化,设计时序深层解析模块(SDP),通过内嵌的时序分解,动态和多次将数据序列分解为趋势部分和周期部分,这种多尺度解析能够帮助模型理解和预测不同时间尺度下的变化规律,提高模型对水质数据长期和短期变化的捕捉能力,从而显著提升预测精度和稳定性。本研究在广东省地表水自动监测网络选取6个点位进行总磷质量浓度预测,对DSC-SDP-TF模型的性能进行评估。
1 数据来源和研究方法 1.1 数据来源和处理 1.1.1 数据来源水质监测数据来自广东省地表水自动监测站点,分别为湛江廉江石角、梅州长沙、石龙北河、永安桥、龙石和沙田泗盛(图 1)。
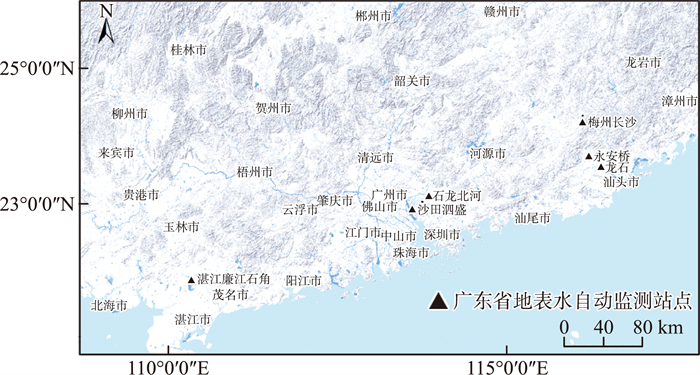
|
图 1 地表水自动监测站点分布 |
每个站点都包含多个同时监测的指标,监测频率为每2或4 h监测1次。总磷是模型预测指标,其他监测指标为特征指标。
1.1.2 数据预处理仪器故障或停电等原因会导致数据的缺失,监测站点也会直接使用一些经验值进行填充(如总磷质量浓度连续多日恒定为0.05 mg/L),导致数据中存在直接填充而非真实监测的数据,即劣质数据。连续多日的缺失或者劣质填充数据会破坏序列趋势,降低模型预测精度[11]。本研究首先对这些劣质填充数据或者缺失数据进行统一处理,被预测指标出现缺失值或者劣质填充值时直接删除;特征数据的缺失或劣质填充比例>70%时直接弃用该特征,否则使用简单的均值填充处理后保留。最终,保留的特征包括:水温、溶解氧、电导率、浊度、高锰酸盐指数、氨氮、铅、铜、锌、镉、氰化物、挥发酚、石油类、蓝绿藻、pH值共15个特征。本研究选择2017—2022年数据作为训练集,2023年数据作为测试集进行模型预测。6个站点的训练集和测试集数据信息见表 1。另外,本研究以湛江廉江石角站为例,展示了训练集和测试集指标的描述统计,结果见表 2。
| 表 1 6个站点的训练集和测试集数据信息 |
| 表 2 湛江廉江石角站训练集和测试集的描述统计 |
本研究采用相关系数分析法,计算15个特征序列和总磷质量浓度的皮尔逊相关系数,绘制热力图(图 2)。以0.05为分界点,筛选出和总磷质量浓度的相关系数绝对值≥0.05的指标,最终保留11个特征,分别为氨氮、高锰酸盐指数、浊度、氰化物、铅、锌、蓝绿藻、石油类、电导率、pH值和溶解氧。
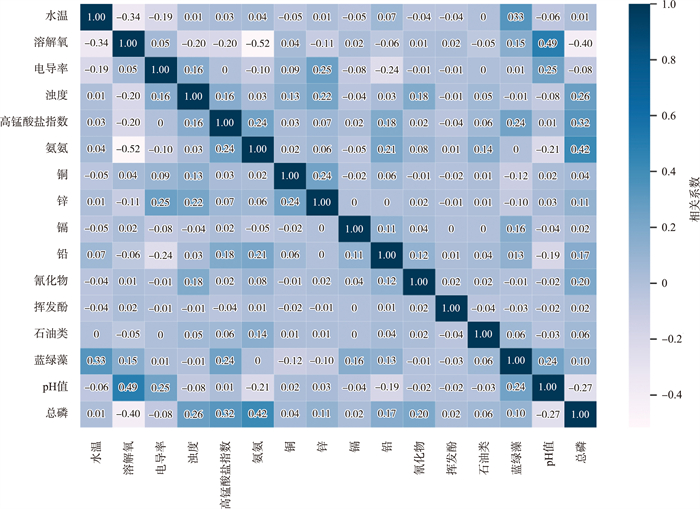
|
图 2 相关系数热力图 |
(1) 水质序列的复杂时变特性
本研究将序列所呈现出的统计特性复杂和难以预测的特点称为复杂时变性。2017—2023年湛江廉江石角站水质序列变化趋势见图 3(a)—(l)。由图 3可见,每个变量都和总磷质量浓度存在潜在的关联。研究时期总磷质量浓度并非简单地围绕平均数值波动,不仅波动的幅度不稳定,潜在趋势也多变难测。其他特征数据亦然。复杂时变性导致无法由过去数据的统计特征推断未来的情况,因而提高了水质数据的建模和预测的难度。
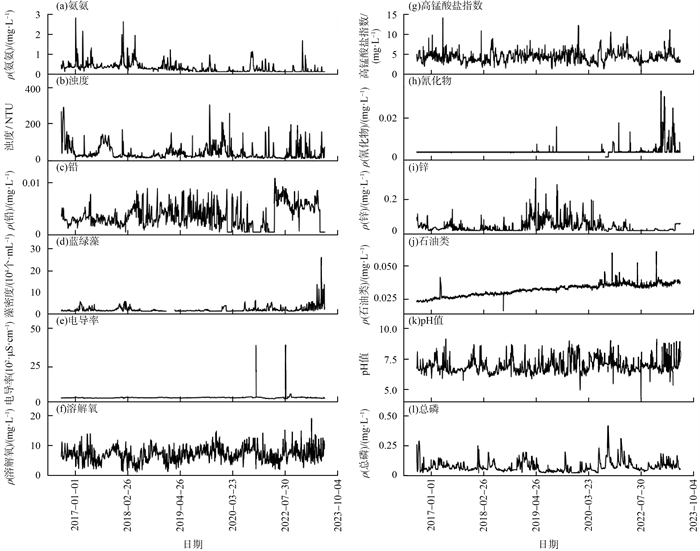
|
图 3 2017—2023年湛江廉江石角站水质序列变化趋势 |
(2) 总磷质量浓度的多尺度动态变化
受到季节等周期性因素的影响,水质数据也呈现出一定程度上的往复变化规律,其变化频率呈现在多个时间尺度。本研究将序列在多个不同时间尺度上呈现出的趋势和周期变化规律统称为多尺度动态变化。2017—2023年湛江廉江石角站总磷质量浓度季度均值变化柱状图和月度变化箱型图见图 4(a)(b)。
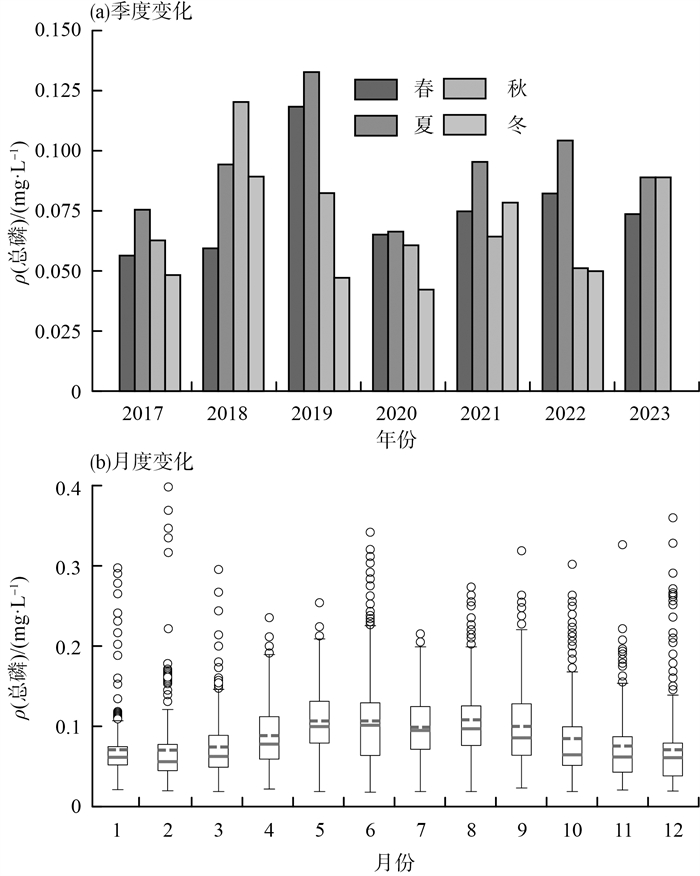
|
图 4 2017—2023年湛江廉江石角站总磷质量浓度季度均值变化柱状图和月度变化箱型图 |
由图 4(a)可见,水质总磷平均质量浓度呈现出夏季最高,春、秋季次之,冬季最低的特点,这可能是由于温度升高时水体中磷化合物的溶解性提高所致[12]。但是这一规律并非一成不变,比如在2019,2020和2022年,水质总磷质量浓度在春、夏最高,秋、冬次之。由图 4(b)可见,总磷月平均质量浓度呈现出单峰分布特征,然而极值分布却极其不稳定。
1.2 研究方法本研究基于水质数据的复杂时变特性和多尺度动态变化,在经典的Transformer模型基础上进行改进,创新地设计了数据稳态调控模块和时序深层解析模块,搭建了适用于水质数据预测问题的DSC-SDP-TF模型。
1.2.1 基础模型Transformer是经典的Seq2Seq模型,包含编码器和解码器。编码器用于感知上下文,将输入序列映射到高维空间,解码器基于上下文,将输入转换成目标序列。Transformer模型框架见图 5。
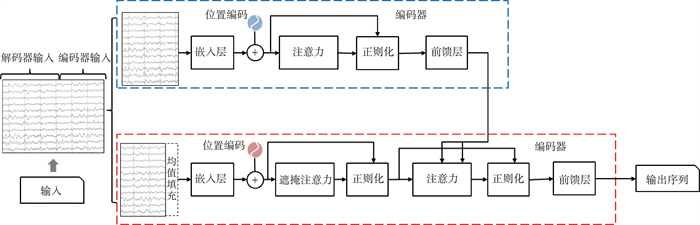
|
图 5 Transformer模型框架 |
Transformer模型的编码器由多个单元堆叠而成。输入序列经过输入表示模块被映射到高维空间,并通过位置编码模块表示先后顺序信息,然后经过多个编码器单元得到上下文表示,每个单元都包含1个自注意力模块和1个前馈神经网络。解码器结构与编码器类似,主要区别在于,解码器单元包含2个注意力模块,第1个为自注意力,采用遮掩机制,第2个利用编码器输出的上下文对第1个注意力模块输出的内容进行解析。
注意力模块是Transformer模型最核心的模块,假设输入序列为X,Qk、Kk和Vk由X通过全连层得到,则第k个注意力头的公式见式(1)和(2)。
| $ \operatorname{Attn}_k\left(Q^{\prime}, K^{\prime}, V^{\prime}\right)=\operatorname{Softmax}\left(\frac{Q_k K_k^T}{\sqrt{d_k}}\right) V_k $ | (1) |
| $ \operatorname{Attention}(X)=\text { Concat }\left(\operatorname{Attn}_1, \cdots, \operatorname{Attn}_n\right) $ | (2) |
(1) 数据稳态调控模块
合理的稳态调控策略能够有效地提高模型预测精度,因此深度学习建模时通常需要将数据进行标准化,然而标准化也会降低注意力模块的表现,针对这一问题,本研究提出数据稳态调控模块(DSC),包括输入稳态调控、输出稳态调控以及注意力稳态调控3个部分。输入和输出稳态调控使得输入和输出序列的分布保持稳定,同时注意力稳态调控辅助减弱标准化的对注意力模块的损害。具体过程如下:
输入数据的形状为X∈
| $ X_i^{\prime}=\frac{X_i-\mu_i}{\sigma_i}, 0 \leqslant i<D $ | (3) |
输入稳态调控中输入数据X′的变换公式见式(4)。
| $ X^{\prime}=\frac{X-\overrightarrow{1} \mu_X}{\overrightarrow{1} \sigma_X} $ | (4) |
其中
输出稳态调控中输出数据Y的变换公式见式(5)。
| $ Y=Y^{\prime} \odot \overrightarrow{1} \sigma_X+\overrightarrow{1} \mu_X $ | (5) |
最后是注意力稳态调控,对于输入序列X∈
| $ \tau=\operatorname{MLP}\left(\sigma_X, X\right) $ | (6) |
| $ \Delta=\operatorname{MLP}\left(\mu_X, X\right) $ | (7) |
| $ \begin{aligned} & \;\;\;\;\;\;\text { DeNormAttention }\left(Q^{\prime}, K^{\prime}, V^{\prime} ; \tau, \Delta\right)= \\ & \operatorname{Softmax}\left(\frac{\tau Q^{\prime} K^{\prime T}+\overrightarrow{1} \Delta^T}{\sqrt{d_k}}\right) V^{\prime} \end{aligned} $ | (8) |
(2) 时序深层解析模块
对于时间序列分析而言,将序列分解为多个部分并有针对性地分析是常用手法[15-16]。水质数据具有多尺度动态变化特性,若直接对输入数据进行时序分解再建模,可能会损失重要信息。本研究设计了嵌入式的时序深层解析模块(SDP)。多个时序解析模块深层嵌入编码器和解码器内部,不断从序列中解析出趋势和周期信息。对于序列X,一个时序解析模块功能见式(9)和(10)。
| $ X_T=\operatorname{AvgPool}[\operatorname{Padding}(X)] $ | (9) |
| $ X_S=X-X_T $ | (10) |
式中:XT——趋势序列;XS——季节周期序列。
2022年1月—2022年12月湛江廉江石角站总磷质量浓度序列分解见图 6。
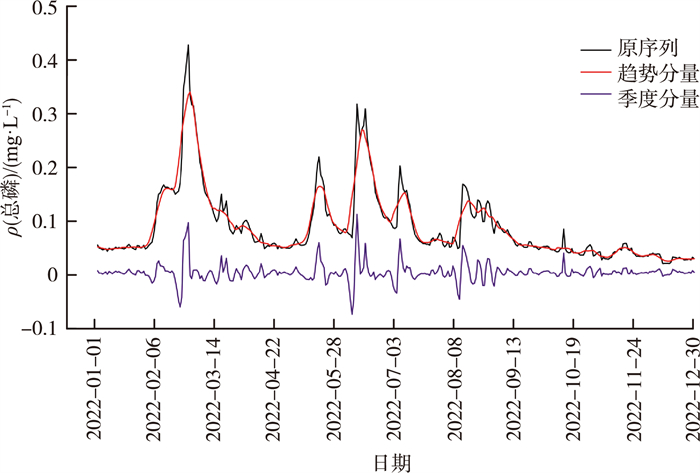
|
图 6 2022年1月—2022年12月湛江廉江石角站总磷质量浓度序列分解 |
(3) DSC-SDP-TF模型框架设计
DSC-SDP-TF模型包含编码器和解码器2个部分,框架设计见图 7。
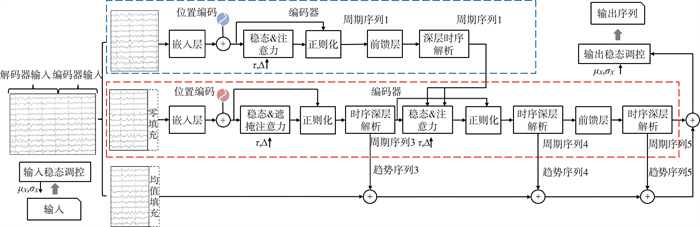
|
图 7 DSC-SDP-TF模型框架设计 |
编码器的输入序列XE经过输入表示和位置编码之后,经过N个编码器单元堆叠处理,最终得到上下文表示。每个编码器单元包含1个注意力模块、1个全连层和2个序列分解模块。令XSl-1为第l-1个子模块输出的季节部分,则第l个子模块的工作概括见式(11)和(12)。
| $ \begin{aligned} & X_S^{l, 1}, _{-}=\text {SeriesDecomp }[\text { DeNormAttention } \\ & \left.\left(Q_S^{l-1}, K_S^{l-1}, V_S^{l-1} ; \tau, \Delta\right)\right] \end{aligned} $ | (11) |
| $ \begin{aligned} & X_S^{l, 2}, _{-}=\text {SeriesDecomp[FeedForward } \\ & \left.\left(X_S^{l, 1}\right)+X_S^{l, 1}\right] \end{aligned} $ | (12) |
式中:QSl-1、KSl-1和VSl-1——均由XSl-1经过线性变换得到。
解码器由1个输入表示模块、1个位置编码模块和多个解码器单元堆叠组成,每个解码器单元包含2个序列分解模块、2个注意力模块和1个全连层。输入序列XD经过输入表示和位置编码之后,被多个内嵌的序列分解模块分为周期部分和趋势部分。周期部分经过N个解码器单元堆叠处理,趋势部分则经过全连层处理并逐步积累,最终2个序列线性加和得到预测序列。令XSl-1为第l-1个子模块输出的周期部分,则第l个子模块的工作概括见式(13)—(16)。
| $ \begin{aligned} & X_S^{l, 1}, X_T^{l, 1}=\text { SeriesDecomp[DeNormMaskAttention } \\ & \left.\left(Q_S^{l-1}, K_S^{l-1}, V_S^{l-1} ; \tau, \Delta\right)\right] \end{aligned} $ | (13) |
| $ \begin{aligned} & X_S^{l, 2}, X_T^{l, 2}=\text { SeriesDecomp[DeNormAttention } \\ & \left.\left(Q_S^{l, 1}, K_{E S}^N, V_{E S}^N ; \tau, \Delta\right)\right] \end{aligned} $ | (14) |
| $ \begin{aligned} & X_S^{l, 3}, X_T^{l, 3}=\text { SeriesDecomp[FeedForward }\left(X_S^{l, 2}\right)+ \\ & \left.X_S^{l, 2}\right] \end{aligned} $ | (15) |
| $ \begin{aligned} & X_T^l=X_T^{l-1}+\operatorname{Linear}\left(X_T^{l, 1}\right)+\operatorname{Linear}\left(X_T^{l, 2}\right)+ \\ & \text { Linear }\left(X_T^{l, 3}\right) \end{aligned} $ | (16) |
式中:QSl-1、KSl-1和VSl-1——均由XSl-1经过线性变换得到;QSl, 1——由XSl, 1经过线性变换得到;KESN和VESN——由编码器输出结果XSN, 2经过线性变换得到;DeNormMaskAttention——经过去平稳化设计且带有遮掩机制的自注意力模块;DeNormAttention——经过去平稳化设计且无遮掩机制的注意力模块。
1.3 评价指标选择对于模型性能,主要选择3个评价指标,分别为均方根误差(RMSE)、平均绝对误差(MAE)和平均百分比误差(MAPE),计算公式见式(17)—(19)。
| $ \text { RMSE }=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2} $ | (17) |
| $ \operatorname{MAE}=\frac{1}{n} \sum\limits_{i=1}^n\left|\hat{y}_i-y_i\right| $ | (18) |
| $ \text { MAPE }=\frac{100 \%}{n} \sum\limits_{i=1}^n\left|\frac{\hat{y}_i-y_i}{y_i}\right| $ | (19) |
式中:n——样本数量;
本研究基于Pytorch框架搭建模型进行实验。模型参数设置如下:输入序列长度为60,嵌入向量维度为64,隐藏层维度为64,DSC-SDP-TF和Transformer模型解码器和编码器单元数量为3,时序分解使用的卷积核大小为7,多头注意力头数为4,每个模型单次训练轮数为200。
2.1 模型预测性能分析根据《地表水环境质量标准》(GB 3838—2002)[17],Ⅰ类地表水总磷质量浓度≤0.02 mg/L,Ⅱ类地表水总磷质量浓度≤0.1 mg/L,优质饮用水的水源需要达到Ⅱ类水质标准。为了让模型保持有效的水质判断,模型误差率须<10%,即模型预测的RMSE和MAE须<0.01 mg/L。
使用DSC-SDP-TF模型分别对6个站点进行1,5和10 d滚动预测,结果见表 3。由表 3可见,从1 d预测结果来看,DSC-SDP-TF模型在6个站点上的1 d预测误差均<0.01 mg/L,平均RMSE为0.005 3 mg/L,平均MAE为0.004 4 mg/L;从5 d预测结果来看,除永安桥之外,其他站点的RMSE和MAE均<0.01 mg/L,平均RMSE为0.008 2 mg/L,平均MAE为0.006 9 mg/L,二者均<0.01 mg/L。因此,DSC-SDP-TF模型能够在至少5 d的时长下精准预测水质总磷质量浓度并对地表水质污染进行预警。
| 表 3 不同预测时长下DSC-SDP-TF模型性能对比 |
综合来看,DSC-SDP-TF模型在石龙北河、梅州长沙和湛江廉江石角这3个站点的预测性能更优,在永安桥、沙田泗盛和龙石这3个站点的预测性能略低于其他站点,尤其在永安桥,1日预测的RMSE为0.009 4 mg/L,远高于其他几个站点,这种差异可以从各站点的地理位置和周围的工业和城市活动强度来解释。
使用Transformer模型和DSC-SDP-TF模型分别对6个站点的水质进行5 d预测,结果见表 4。由表 4可见,DSC-SDP-TF模型在6个站点上5 d预测的RMSE平均值为0.008 2 mg/L,相比于Transfomer模型提升了36.66%,MAE平均值为0.006 9 mg/L,相比于Transformer模型提升了38.37%,MAPE平均值为6.14%,相比于Transformer模型提升了37.08%。3个维度测量的性能提升均在38%左右,说明DSC-SDP-TF模型在水质预测上表现更出色。
| 表 4 DSC-SDP-TF模型和Transformer模型性能对比 |
2023年3—10月6个站点水体总磷质量浓度的1 d和5 d滚动预测结果见图 8(a)—(f)。由图 8可见,从1日的预测结果来看,DSC-SDP-TF模型和Transformer模型的预测结果都与原总磷质量浓度趋势较为贴合,但当序列震荡较为剧烈时[图 8(a)(b)中虚线框部分],DSC-SDP-TF模型的预测能力优于Transformer模型,这是因为DSC-SDP-TF模型中的平稳化机制设计使得模型在震荡数据上表现更为稳健;从5 d预测结果来看,Transformer模型的预测结果较差,而DSC-SDP-TF模型仍然可以保持较高的精度[图 8(b)(d)中虚线框部分],这是由于DSC-SDP-TF模型中的序列分解机制设计,使其能够精准地捕捉中长期趋势,在中长期预测上性能更加稳定。最后,不同的站点纵向比较,永安桥的预测难度最高,这一点和表 3的结论一致,此时Transformer模型的1 d和5 d预测能力都较差,DSC-SDP-TF模型的1 d预测仍然能够较为精准地贴合原序列,5 d预测效果远远优于Transformer模型,说明DSC-SDP-TF模型在劣质数据上依然能够保持稳定的性能。
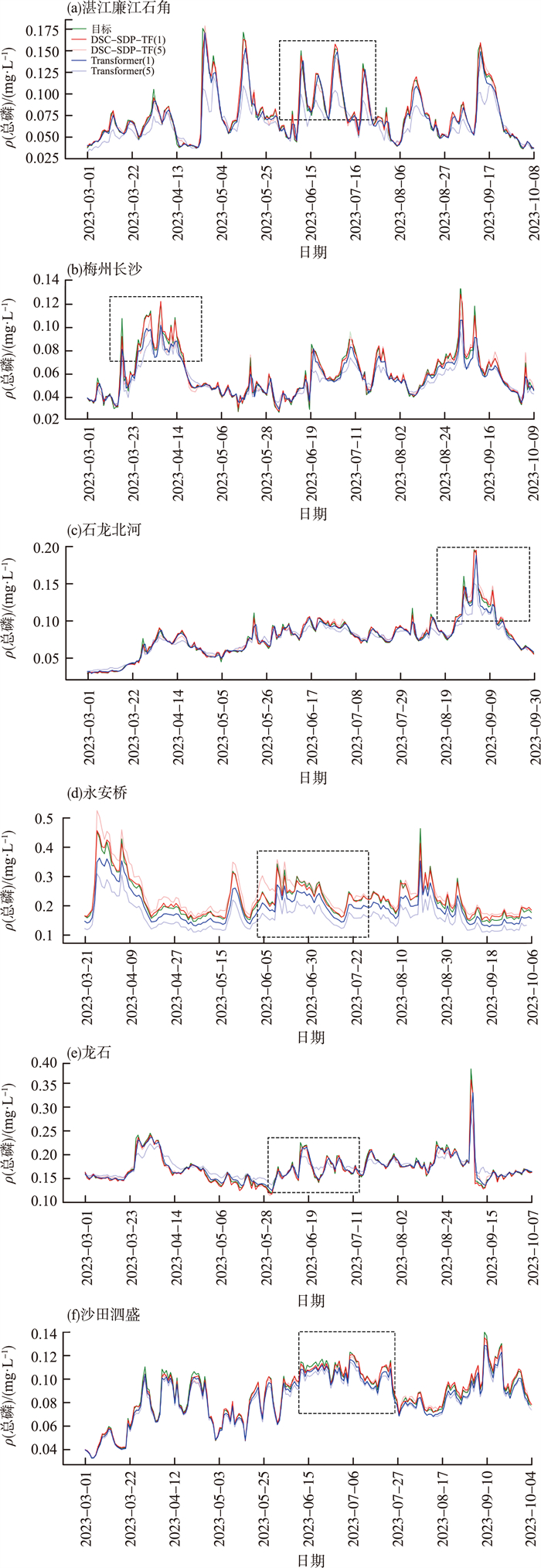
|
图 8 2023年3—10月6个站点水体总磷质量浓度的1日和5日滚动预测结果 |
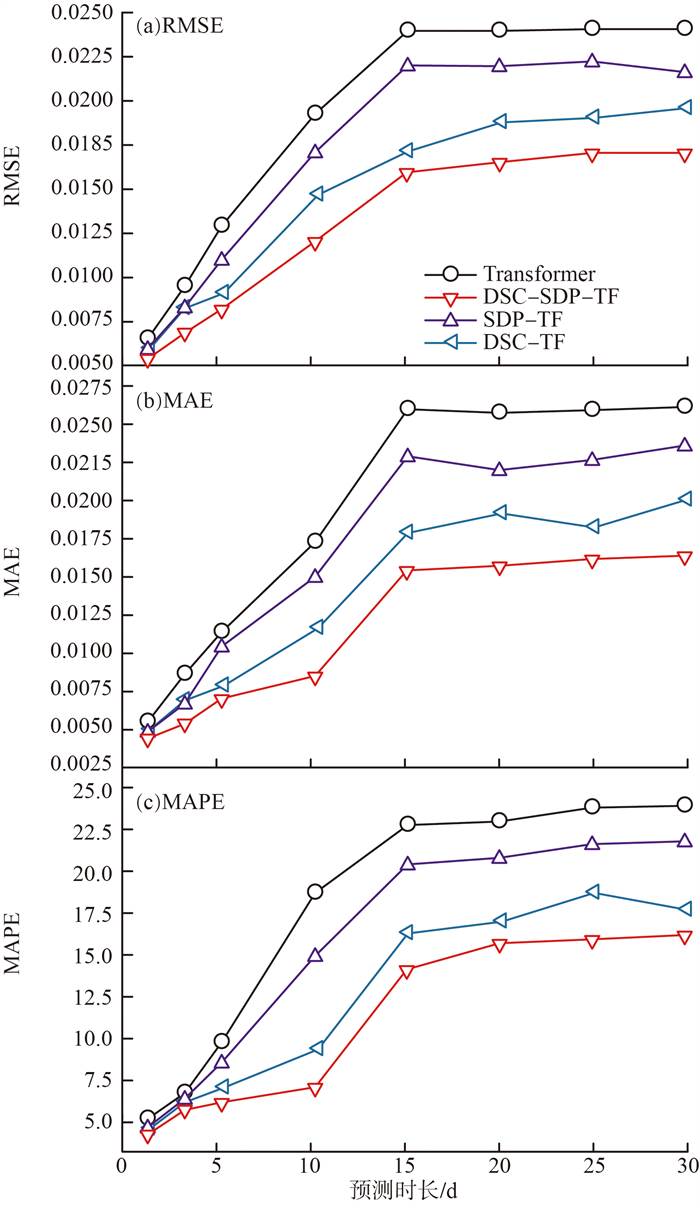
消融实验是深度学习中验证模型有效性的重要方法之一,主要是通过逐步移除模型中某些结构(模块或者特征等)并观察模型性能变化,来分析这些结构对模型性能的贡献。本研究在Transformer模型的基础上,分别单独增加数据稳态调控模块和时序深层解析模块,构成DSC-TF和SDP-TF这2个模型,和本研究搭建的DSC-SDP-TF模型以及传统的Transformer模型进行对比。4种模型1~30 d预测消融实现结果见图 9(a)—(c)。由图 9可见,深层时序解析结构和数据稳态调控结构均能有效提升Transformer模型的性能,且数据稳态调控结构对模型性能的提升优于时序深层解析结构。
|
图 9 4种模型1~30 d预测消融实验结果 |
本研究通过Python 3.9环境搭建DSC-SDP-TF模型,基于广东省6个地表水监测站点的水质监测数据,对总磷质量浓度进行预测,并与相同参数下的Transformer模型进行对比,主要结论如下。
(1) 从DSC-SDP-TF模型的预测精度上来看,1 d和5 d预测的平均误差均<0.01 mg/L。表明该模型至少能在10%的误差水平上对Ⅱ类地表水总磷质量浓度进行预测和监控。
(2) 从DSC-SDP-TF模型和Transformer模型的效果对比来看,DSC-SDP-TF模型3个指标的平均性能提升幅度均为38%左右,说明该模型在水质预测方面相较于Transformer模型有较大幅度的提升。
(3) 从6个站点的预测效果来看,除了永安桥外,其他站点的1 d和5 d预测曲线均较为贴合原曲线。当数据波动性较大或预测时长较长时,DSC-SDP-TF模型能够表现出更加优越和稳定的性能。
(4) 从消融实验来看,数据稳态调控结构和时序深层解析结构均有效增加了Transformer架构的预测能力,且数据稳态调控结构的贡献更明显。
3.2 不足和展望(1) 从模型层面看,DSC-SDP-TF模型在引入数据稳态调控模块和时序深层解析模块后,显著提高了预测性能,但也增加了模型的计算复杂性和计算成本。未来研究可能通过模型压缩、参数剪枝或高效计算架构来优化模型的计算效率。
(2) 从现实层面看,DSC-SDP-TF模型在具有更高波动性和复杂性的沿海水域环境中仍有提升空间。未来研究可以考虑进一步优化模型结构,提高模型稳健性。
| [1] |
生态环境部. 2022年第四季度和1—12月全国地表水环境质量状况[R]. 北京: 生态环境部, 2023.
|
| [2] |
张亚丽, 王艺铭, 史淑娟, 等. 基于QUAL2K模型的鹤壁卫河水质模拟预警研究[J]. 中国环境监测, 2018, 34(5): 138-143. |
| [3] |
JI Z G. Hydrodynamics and water quality: Modeling rivers, lakes, and estuaries[C]. Proceedings of the International Conference on Environmental Science and Technology, 2017: 100-110.
|
| [4] |
KELLER V. Risk assessment of "down-the-drain" chemicals: Search for a suitable model[J]. Science of The Total Environment, 2006, 360(1): 305-318. |
| [5] |
BARZEGAR R, AALAMI M T, ADAMOWSKI J. Short-term water quality variable prediction using a hybrid CNN-LSTM deep learning model[J]. Stochastic Environmental Research and Risk Assessment, 2020, 34(2): 415-433. |
| [6] |
张贻婷, 李天宏. 基于长短时记忆神经网络的河流水质预测研究[J]. 环境科学与技术, 2021, 44(8): 163-169. |
| [7] |
PANG J, LUO W, YAO Z, et al. Water quality prediction in urban waterways based on wavelet packet denoising and LSTM[J]. Water Resources Management, 2024, 38(2): 2399-2420. |
| [8] |
马志峰, 张浩, 刘劼. 基于深度学习的短临降水预报综述[J]. 计算机工程与科学, 2023, 45(10): 1731-1753. DOI:10.3969/j.issn.1007-130X.2023.10.003 |
| [9] |
ZHANG Q, YOU X Y. Recent advances in surface water quality prediction using artificial intelligence models[J]. Water Resources Management, 2024, 38(2): 235-250. |
| [10] |
YAO S Y, ZHANG Y H, WANG P, et al. Long-term water quality prediction using integrated water quality indices and advanced deep learning models: A case study of Chaohu Lake, China, 2019—2022[J]. Applied Sciences, 2022, 12(22): 11329. |
| [11] |
ROCHA P, SANTOS V, THÉ J, et al. New graph-based and transformer deep learning models for river dissolved oxygen forecasting[J]. Environments, 2023, 10(12): 217. |
| [12] |
WANG H, ZHANG L, WU R, et al. Enhancing dissolved oxygen concentrations prediction in water bodies: A temporal transformer approach with multi-site meteorological data graph embedding[J]. Water, 2023, 15(17): 3029. |
| [13] |
TRIPATHY K, MISHRA A. Deep learning in hydrology and water resources disciplines: Concepts, methods, applications, and research directions[J]. Journal of Hydrology, 2024, 628: 130458. |
| [14] |
WU X, ZHANG Q, WEN F, et al. A water quality prediction model based on multi-task deep learning: A case study of the Yellow River, China[J]. Water, 2022, 14(21): 3408. |
| [15] |
CLEVELAND R B, CLEVELAND W S, MCRAE J E, et al. STL: A seasonal-trend decomposition procedure based on Loess[J]. Journal of Official Statistics, 1990, 6(1): 3-73. |
| [16] |
BANDARA K, HYNDMAN R J, BERGMEIR C. MSTL: A seasonal-trend decomposition algorithm for time series with multiple seasonal patterns[J]. International Journal of Forecasting, 2021, 37(3): 1185-1193. |
| [17] |
中华人民共和国国家环境保护总局, 国家质量监督检验检疫总局. 地表水环境质量标准: GB 3838—2002[S]. 北京: 中国环境科学出版社, 2002.
|
 2025, Vol. 17
2025, Vol. 17 